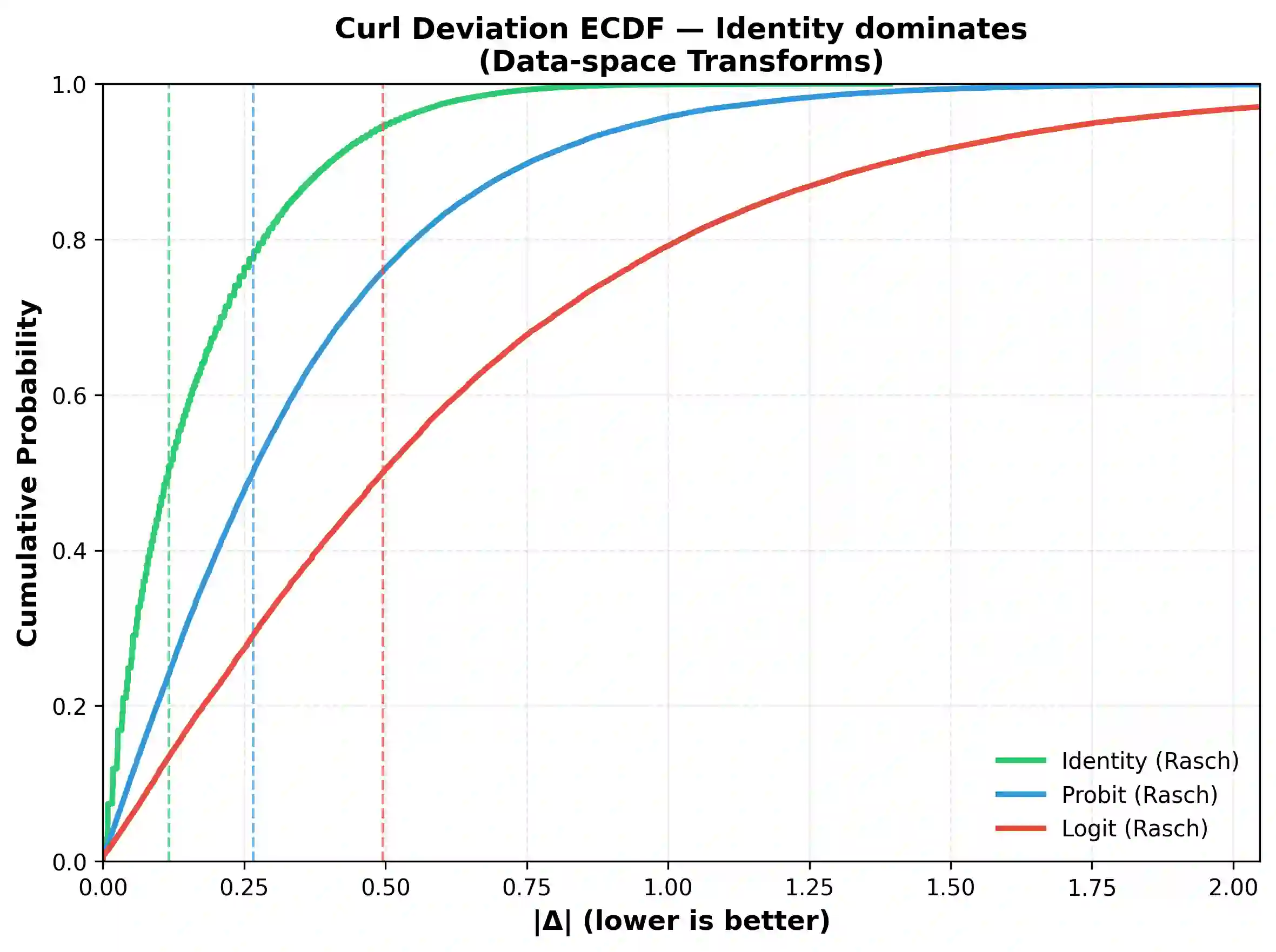
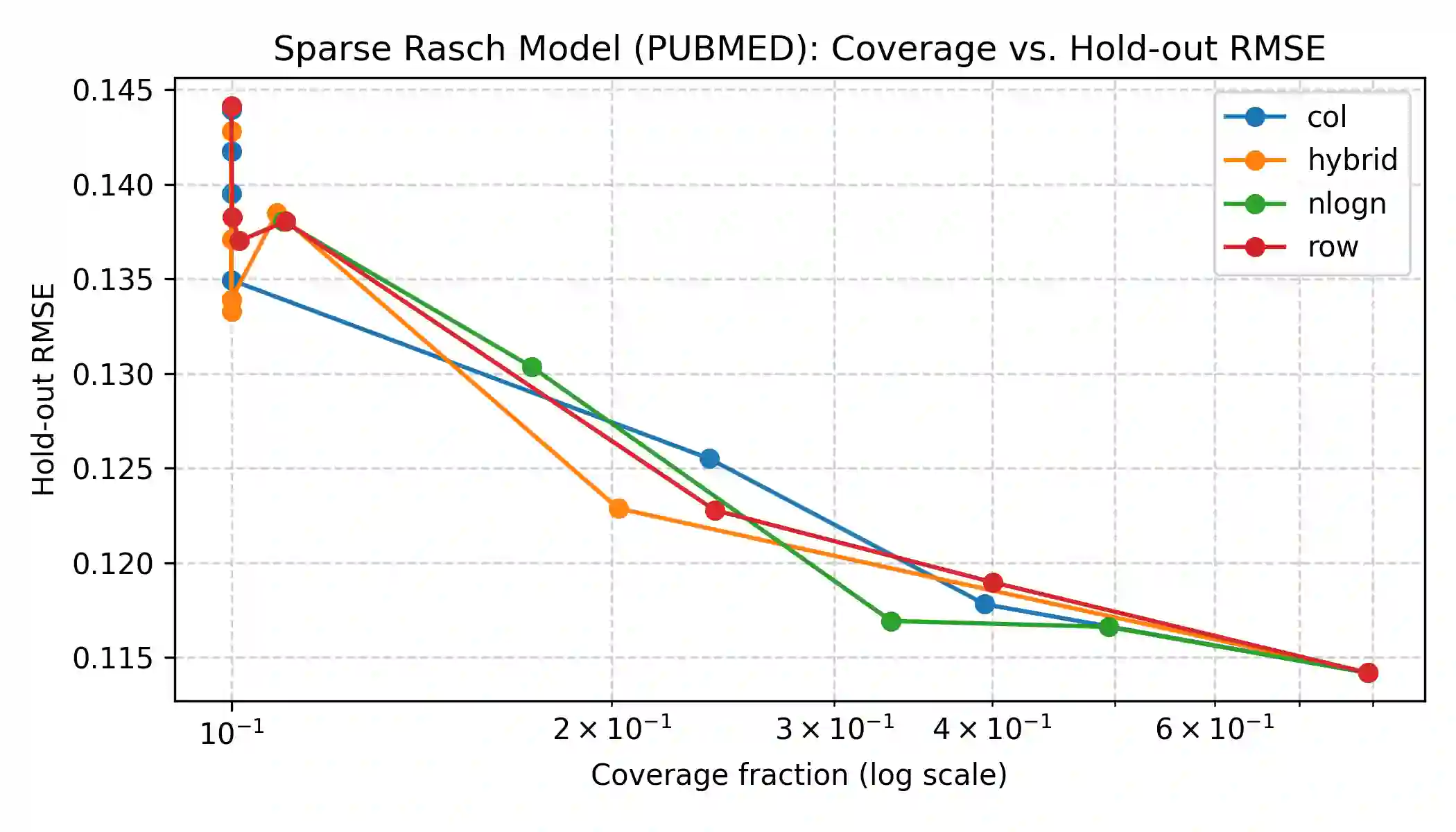
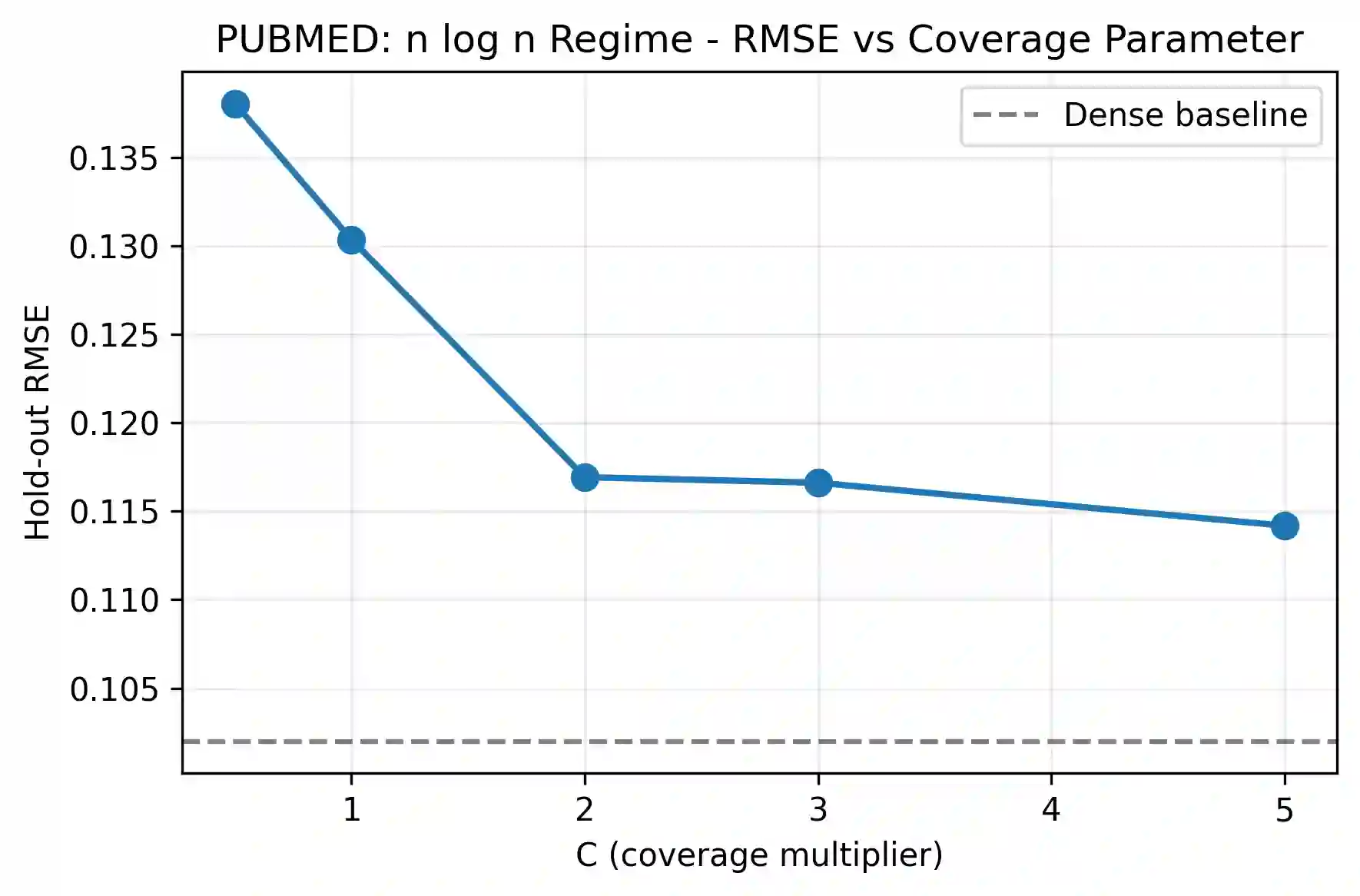
Pairwise comparisons of large language models using total variation distance mutual information (TVD-MI) produce binary critic decisions per pair. We show that averaging TVD-MI's binary trials yields centered-probability scores with additive structure suitable for item-response theory (IRT) without nonlinear link functions. Maximum-likelihood approaches to IRT use logistic links, but we find empirically that these transformations introduce curvature that breaks additivity: across three domains, the identity link yields median curl on raw data of 0.080-0.150 (P95 = [0.474, 0.580]), whereas probit/logit introduce substantially higher violations (median [0.245, 0.588], P95 [0.825, 2.252]). We derive this clipped-linear model from Gini entropy maximization, yielding a box-constrained least-squares formulation that handles boundary saturation. At 33% coverage, we achieve holdout RMSE $0.117 \pm 0.008$ while preserving agent rankings (Spearman $\rho = 0.972 \pm 0.015$), three times fewer evaluations than full dense. Judge robustness analysis (GPT-4o-mini vs. Llama3-70b) shows strong agreement in agent rankings ($\rho = 0.872$) and consistent identity-link advantage. TVD-MI's geometry is best preserved by identity mapping for efficient LLM evaluation, applicable to other bounded-response domains.

翻译：使用总变差距离互信息（TVD-MI）对大语言模型进行成对比较时，每对模型产生二元评判决策。我们证明，对TVD-MI的二元试验结果进行平均可得到具有可加性结构的中心化概率分数，该结构适用于无需非线性链接函数的项目反应理论（IRT）。IRT的最大似然方法通常采用逻辑链接函数，但我们通过实证发现这些变换会引入曲率破坏可加性：在三个领域中，原始数据上恒等链接产生的曲率中位数为0.080-0.150（P95 = [0.474, 0.580]），而概率单位/逻辑链接则导致显著更高的违例（中位数[0.245, 0.588]，P95 [0.825, 2.252]）。我们从基尼熵最大化推导出该截断线性模型，得到能够处理边界饱和问题的箱型约束最小二乘公式。在33%覆盖率下，我们实现了留出集均方根误差 $0.117 \pm 0.008$，同时保持智能体排序（斯皮尔曼 $\rho = 0.972 \pm 0.015$），评估次数比完全稠密设计减少三分之二。评判者稳健性分析（GPT-4o-mini 与 Llama3-70b）显示智能体排序高度一致（$\rho = 0.872$）且恒等链接优势具有一致性。TVD-MI的几何特性通过恒等映射得以最佳保持，从而实现高效的大语言模型评估，该方法可推广至其他有界响应领域。