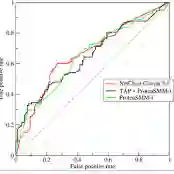
In medical diagnostics, leveraging multiple biomarkers can significantly improve classification accuracy compared to using a single biomarker. While existing methods based on exponential tilting or density ratio models have shown promise, their assumptions may be overly restrictive in practice. In this paper, we adopt a flexible semiparametric model that relates the density ratio of diseased to healthy subjects through an unknown monotone transformation of a linear combination of biomarkers. To enhance estimation efficiency, we propose a smoothed likelihood framework that exploits the smoothness in the underlying densities and transformation function. Building on the maximum smoothed likelihood methodology, we construct estimators for the model parameters and the associated probability density functions. We develop an effective computational algorithm for implementation, derive asymptotic properties of the proposed estimators, and establish procedures for estimating the receiver operating characteristic (ROC) curve and the area under the curve (AUC). Through simulation studies and a real-data application, we demonstrate that the proposed method yields more accurate and efficient estimates than existing approaches.

翻译：在医学诊断中，利用多种生物标志物相较于单一生物标志物可显著提高分类准确性。尽管基于指数倾斜或密度比模型的现有方法已显示出潜力，但其假设在实践中可能过于严格。本文采用一种灵活的半参数模型，该模型通过生物标志物线性组合的未知单调变换来关联患病与健康受试者的密度比。为提高估计效率，我们提出一种平滑似然框架，该框架利用基础密度函数与变换函数的光滑性。基于最大平滑似然方法，我们构建了模型参数及相关概率密度函数的估计量。我们开发了一种高效的计算算法用于实现，推导了所提估计量的渐近性质，并建立了估计接收者操作特征（ROC）曲线及曲线下面积（AUC）的流程。通过模拟研究和实际数据应用，我们证明所提方法相较于现有方法能产生更准确、更高效的估计。