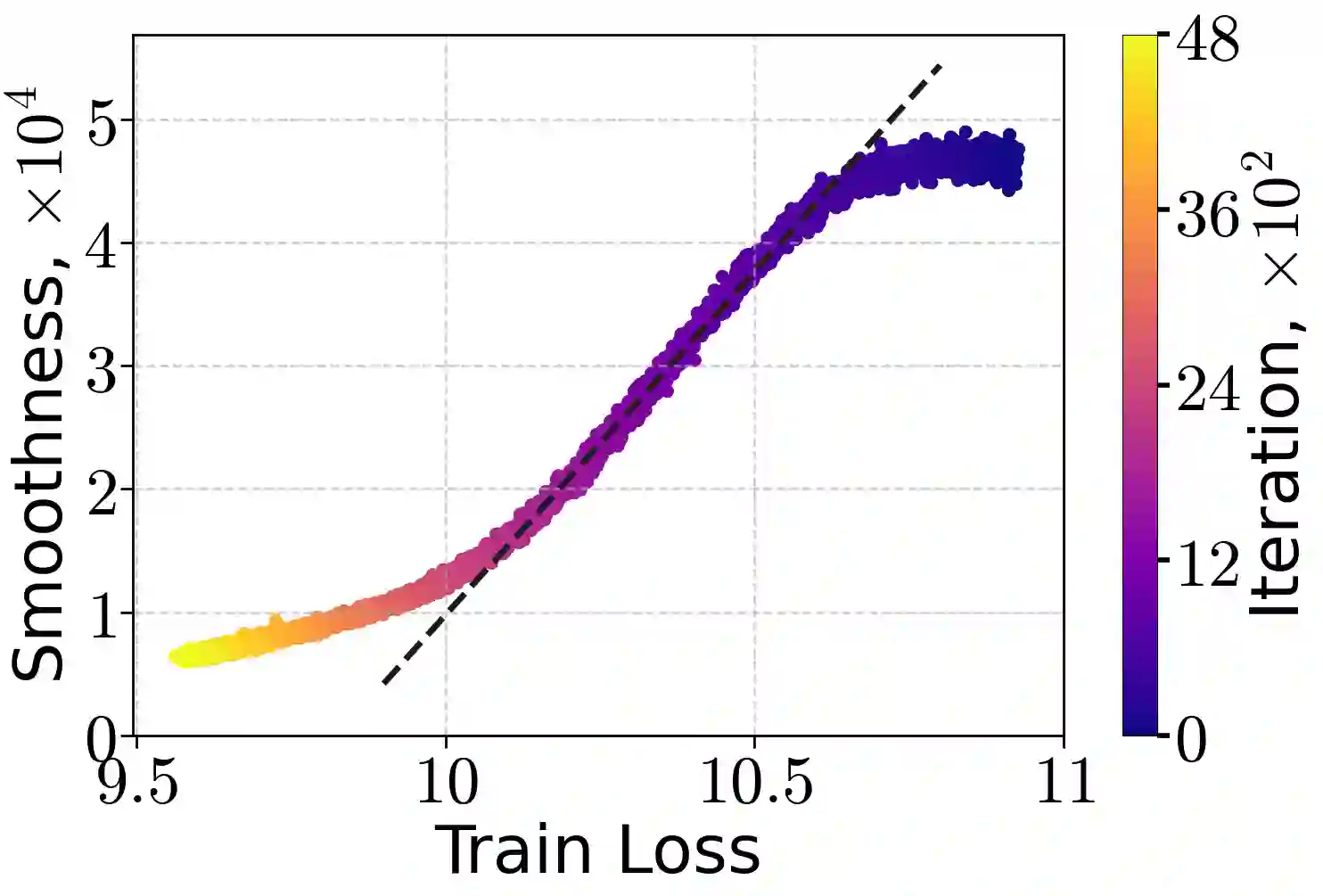
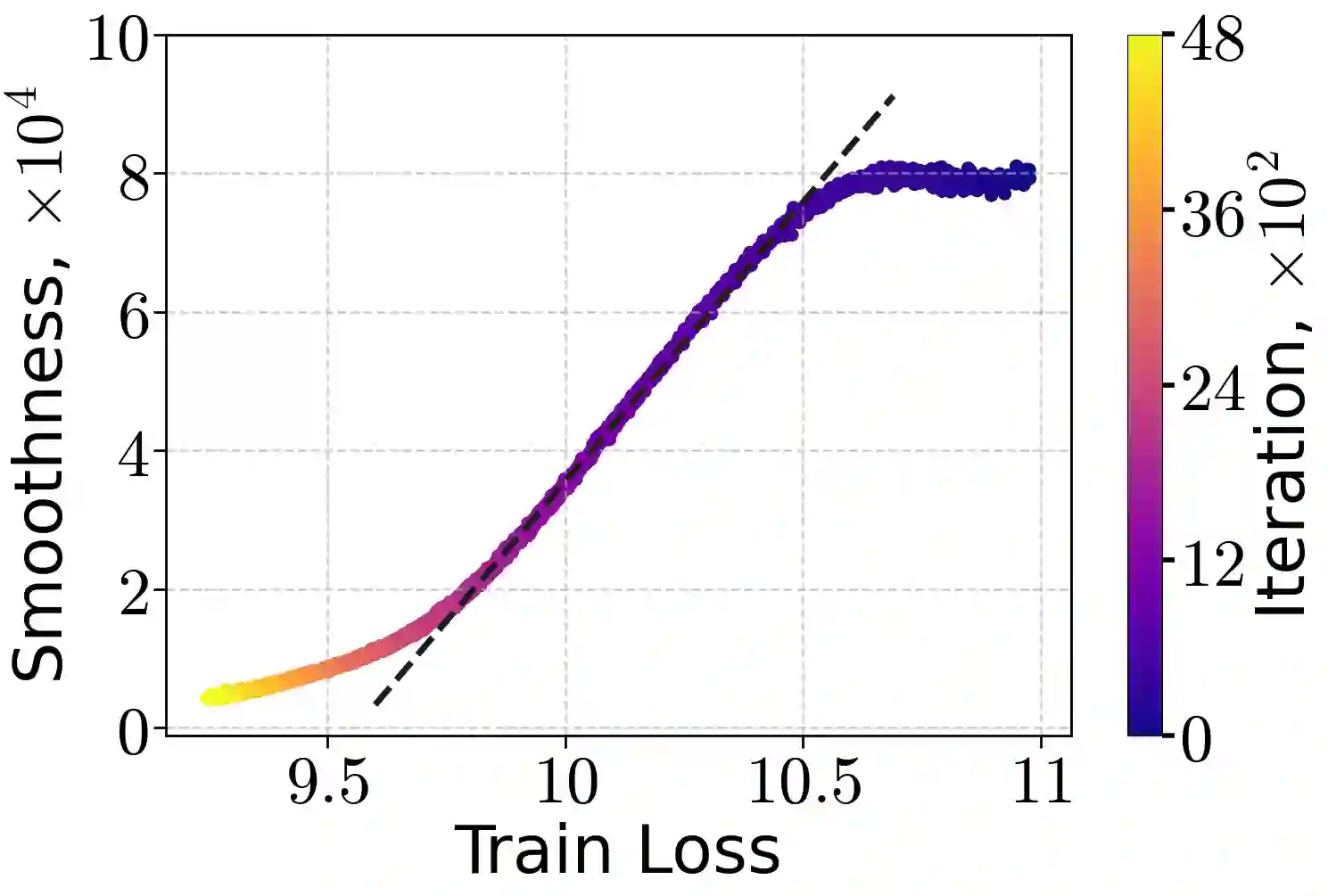
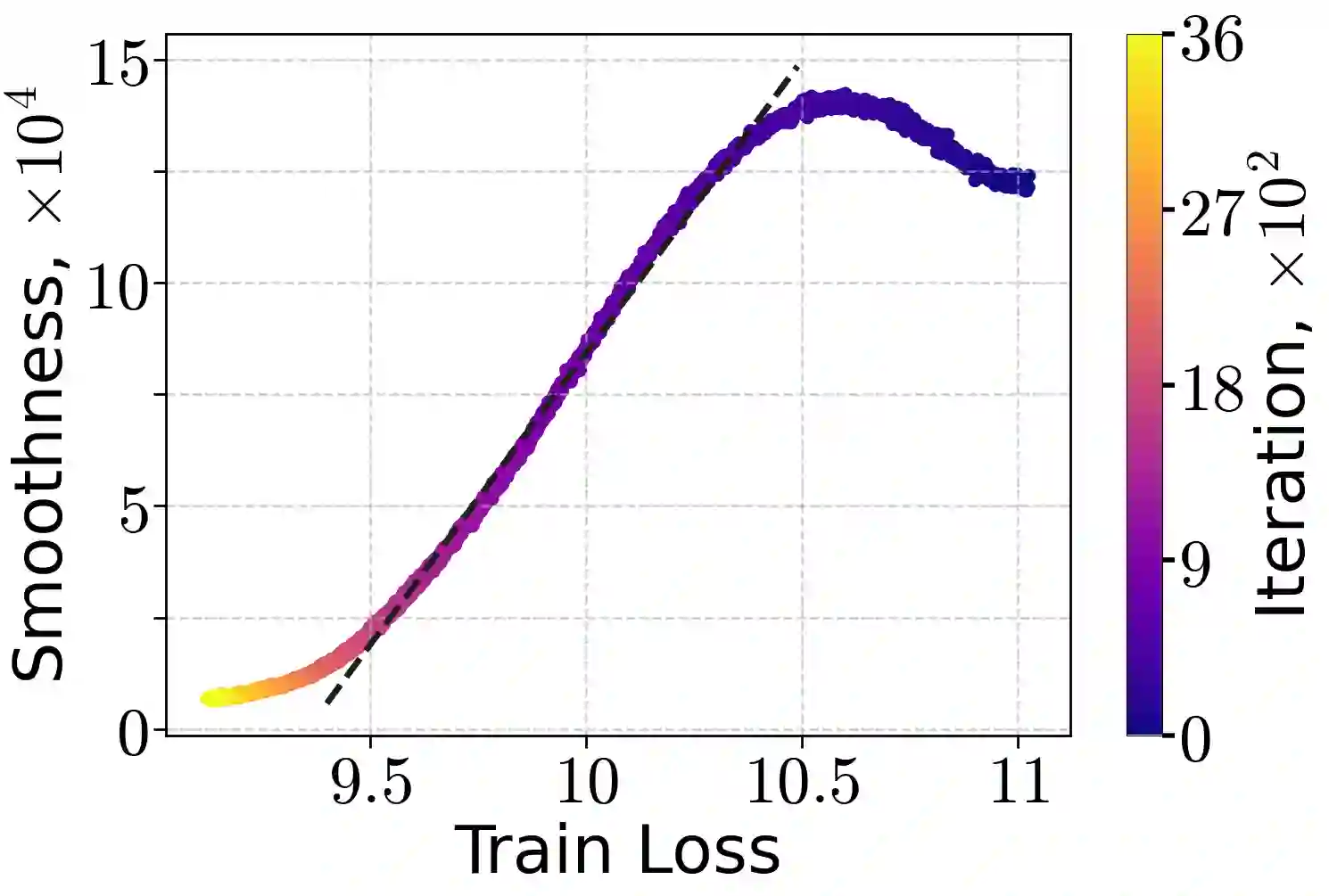
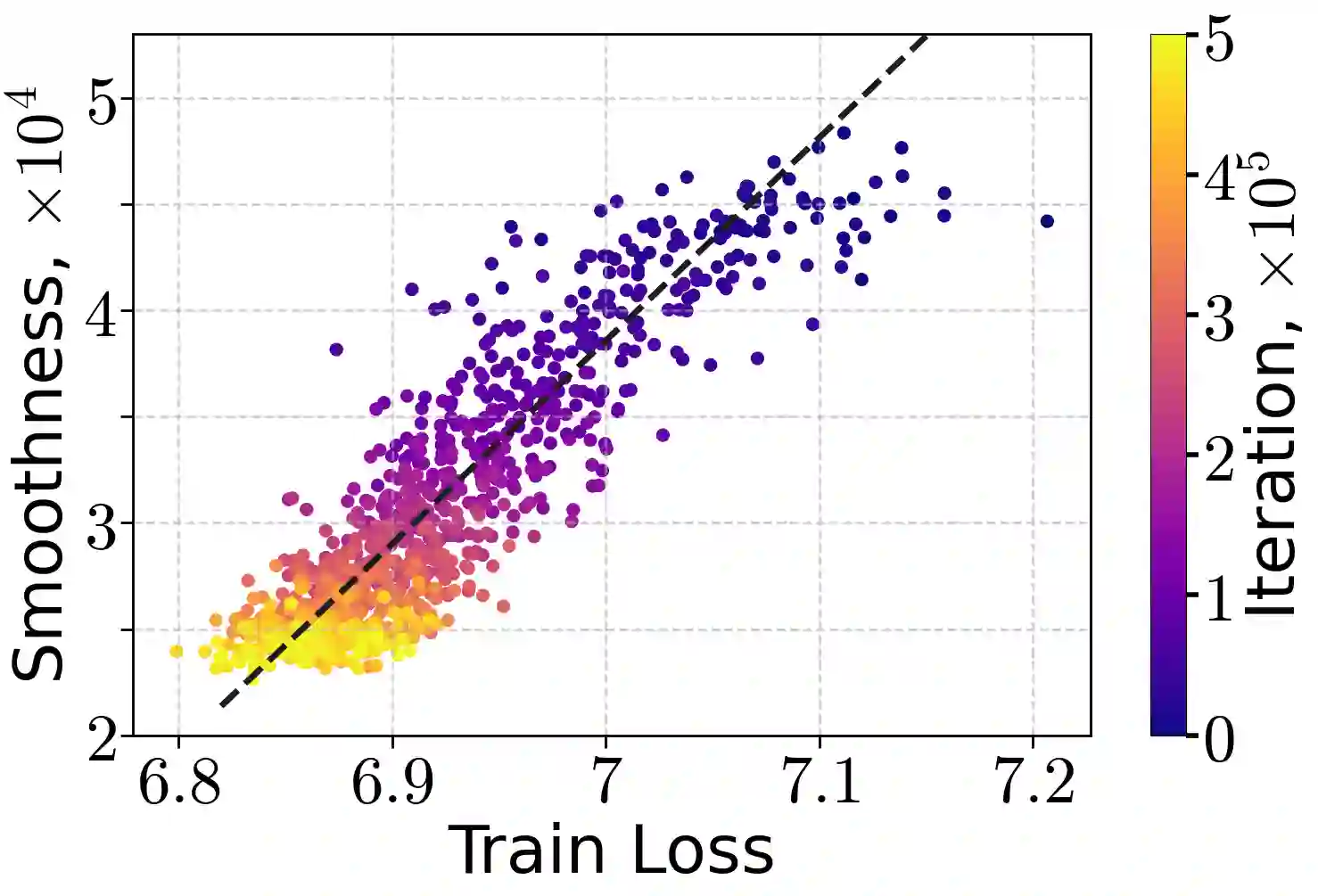
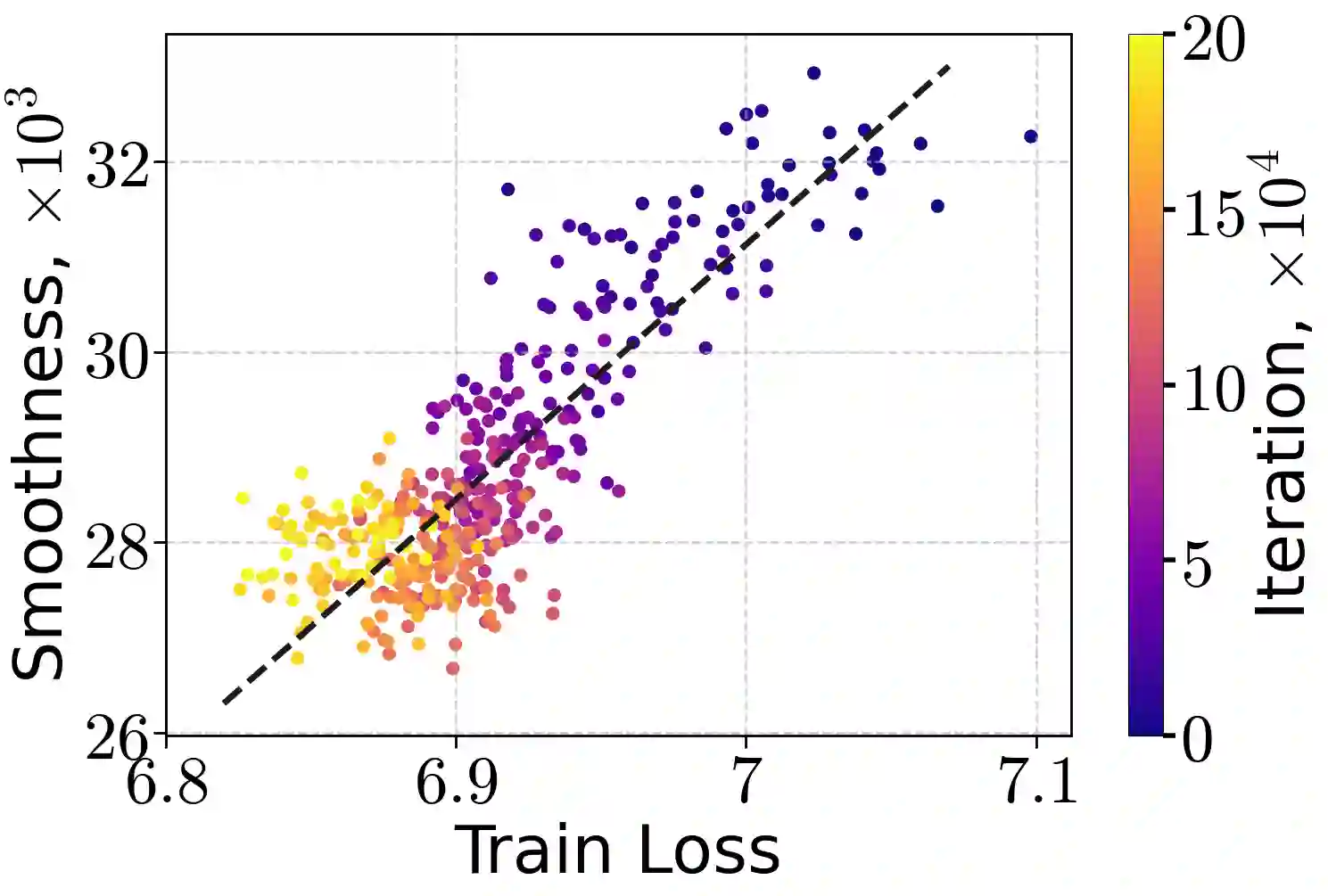
Learning rate warm-up - increasing the learning rate at the beginning of training - has become a ubiquitous heuristic in modern deep learning, yet its theoretical foundations remain poorly understood. In this work, we provide a principled explanation for why warm-up improves training. We rely on a generalization of the $(L_0, L_1)$-smoothness condition, which bounds local curvature as a linear function of the loss sub-optimality and exhibits desirable closure properties. We demonstrate both theoretically and empirically that this condition holds for common neural architectures trained with mean-squared error and cross-entropy losses. Under this assumption, we prove that Gradient Descent with a warm-up schedule achieves faster convergence than with a fixed step-size, establishing upper and lower complexity bounds. Finally, we validate our theoretical insights through experiments on language and vision models, confirming the practical benefits of warm-up schedules.

翻译：学习率预热——在训练初期逐步增加学习率——已成为现代深度学习中普遍采用的启发式策略，但其理论基础仍未得到充分理解。本文从原理层面解释了预热策略为何能改善训练效果。我们基于对$(L_0, L_1)$-光滑条件的推广展开分析，该条件将局部曲率约束为损失次优度的线性函数，并展现出良好的封闭性质。我们通过理论证明和实验验证，表明该条件对于采用均方误差和交叉熵损失训练的常见神经网络架构均成立。在此假设下，我们证明了采用预热策略的梯度下降法比固定步长方法具有更快的收敛速度，并建立了复杂度的上下界。最后，我们通过在语言和视觉模型上的实验验证了理论发现，证实了预热策略的实际效益。