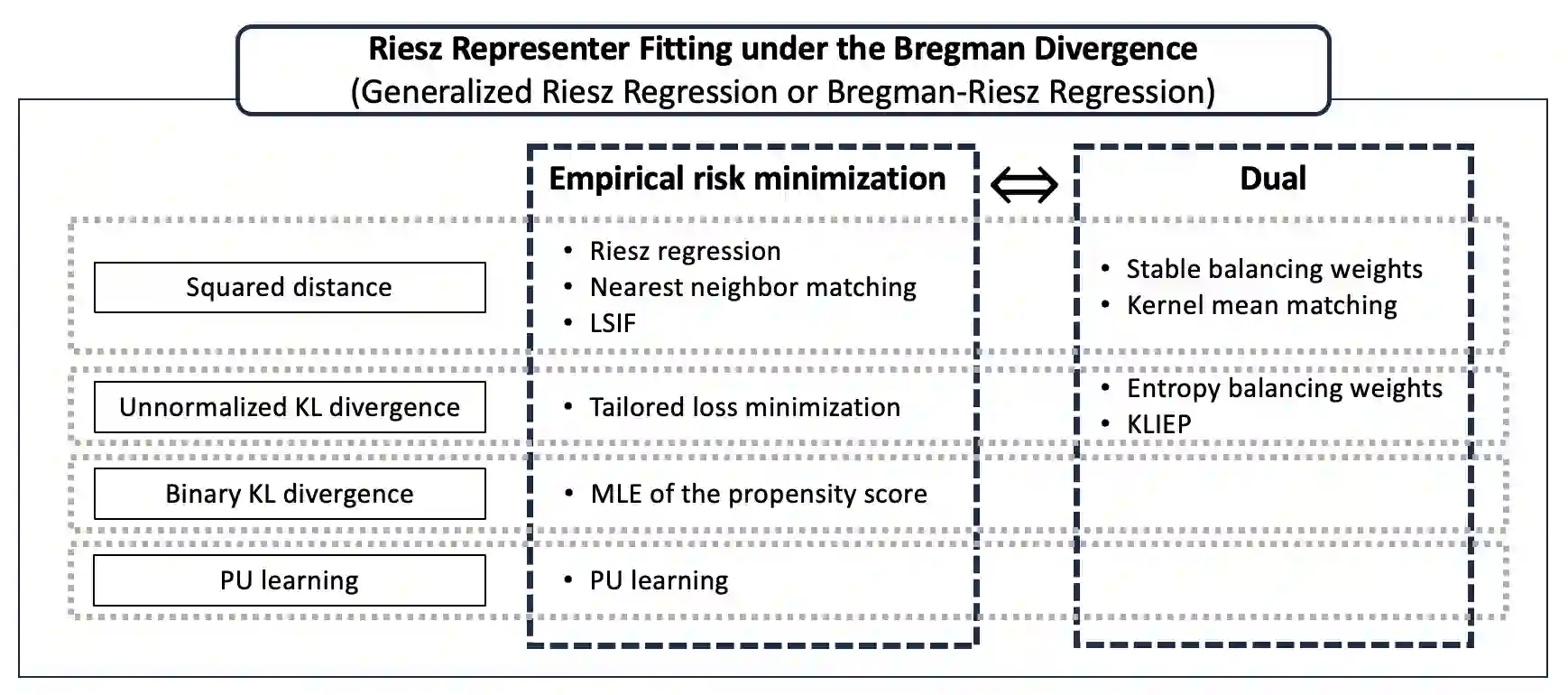
Estimating the Riesz representer is a central problem in debiased machine learning for causal and structural parameter estimation. Various methods for Riesz representer estimation have been proposed, including Riesz regression and covariate balancing. This study unifies these methods within a single framework. Our framework fits a Riesz representer model to the true Riesz representer under a Bregman divergence, which includes the squared loss and the Kullback--Leibler (KL) divergence as special cases. We show that the squared loss corresponds to Riesz regression, and the KL divergence corresponds to tailored loss minimization, where the dual solutions correspond to stable balancing weights and entropy balancing weights, respectively, under specific model specifications. We refer to our method as generalized Riesz regression, and we refer to the associated duality as automatic covariate balancing. Our framework also generalizes density ratio fitting under a Bregman divergence to Riesz representer estimation, and it includes various applications beyond density ratio estimation. We also provide a convergence analysis for both cases where the model class is a reproducing kernel Hilbert space (RKHS) and where it is a neural network.

翻译：估计 Riesz 表示元是用于因果和结构参数估计的去偏机器学习中的一个核心问题。目前已提出了多种 Riesz 表示元估计方法，包括 Riesz 回归和协变量平衡。本研究将这些方法统一在一个框架内。我们的框架在 Bregman 散度下，将 Riesz 表示元模型拟合到真实的 Riesz 表示元，该散度以平方损失和 Kullback–Leibler (KL) 散度作为特例。我们证明，平方损失对应于 Riesz 回归，而 KL 散度对应于定制损失最小化，其中在对特定模型设定的情况下，其对偶解分别对应于稳定平衡权重和熵平衡权重。我们将我们的方法称为广义 Riesz 回归，并将相关的对偶性称为自动协变量平衡。我们的框架还将 Bregman 散度下的密度比拟合推广到 Riesz 表示元估计，并且包含了密度比估计之外的多种应用。我们还对模型类为再生核希尔伯特空间 (RKHS) 以及模型类为神经网络两种情况提供了收敛性分析。