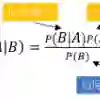
Due to its linear complexity, naive Bayes classification remains an attractive supervised learning method, especially in very large-scale settings. We propose a sparse version of naive Bayes, which can be used for feature selection. This leads to a combinatorial maximum-likelihood problem, for which we provide an exact solution in the case of binary data, or a bound in the multinomial case. We prove that our convex relaxation bounds becomes tight as the marginal contribution of additional features decreases, using a priori duality gap bounds dervied from the Shapley-Folkman theorem. We show how to produce primal solutions satisfying these bounds. Both binary and multinomial sparse models are solvable in time almost linear in problem size, representing a very small extra relative cost compared to the classical naive Bayes. Numerical experiments on text data show that the naive Bayes feature selection method is as statistically effective as state-of-the-art feature selection methods such as recursive feature elimination, $l_1$-penalized logistic regression and LASSO, while being orders of magnitude faster.

翻译：由于其线性复杂度，朴素贝叶斯分类仍然是一种有吸引力的监督学习方法，尤其是在超大规模场景中。我们提出了一种稀疏版本的朴素贝叶斯，可用于特征选择。这导出了一个组合最大似然问题，我们针对二元数据情况给出了精确解，或在多项情况下给出了一个界。利用从沙普利-福克曼定理导出的先验对偶间隙界，我们证明了当额外特征的边际贡献减小时，我们的凸松弛界会变得紧致。我们展示了如何生成满足这些界的原始解。无论是二元还是多项稀疏模型，其求解时间几乎与问题规模呈线性关系，相较于经典朴素贝叶斯，仅增加了极小的额外相对成本。在文本数据上的数值实验表明，朴素贝叶斯特征选择方法在统计效能上与递归特征消除、$l_1$惩罚逻辑回归和LASSO等最先进的特征选择方法相当，同时计算速度快数个数量级。