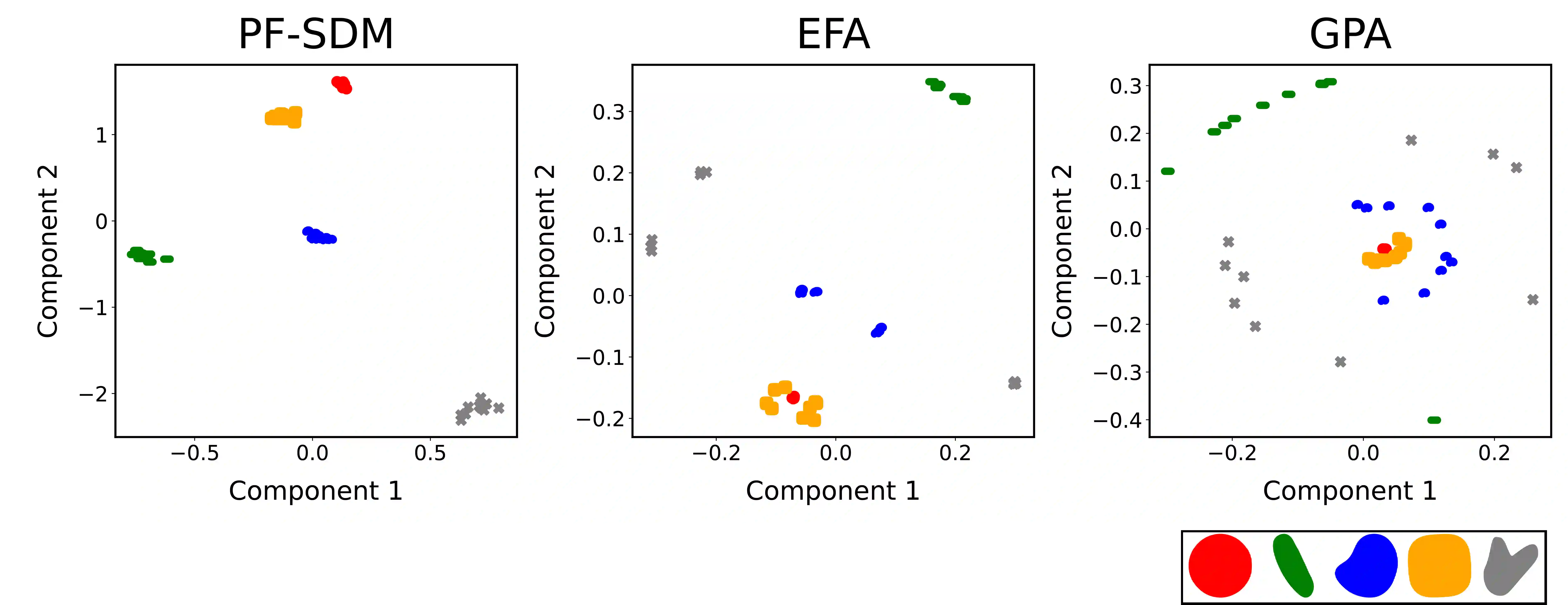
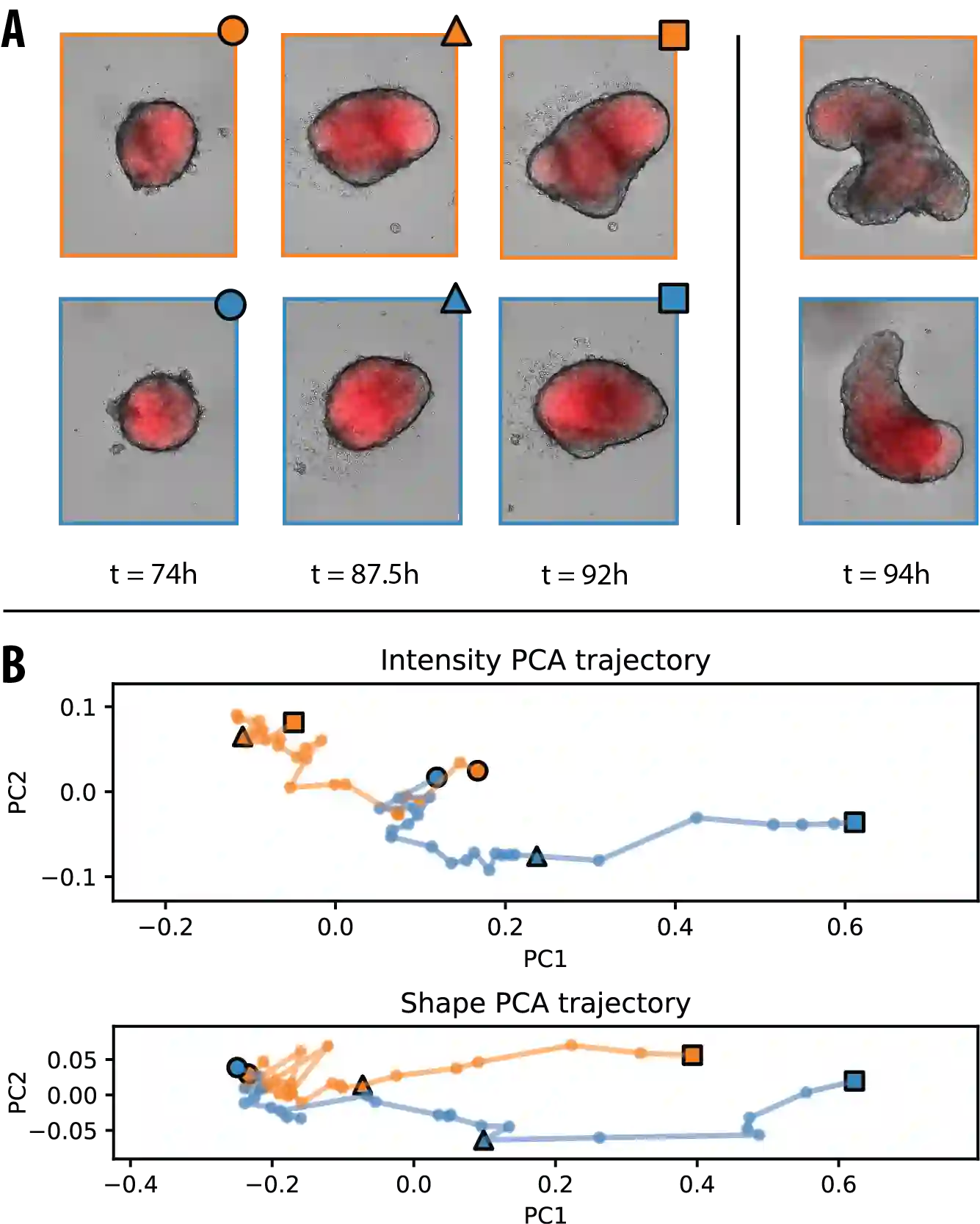
We introduce the Push-Forward Signed Distance Morphometric (PF-SDM) for shape quantification in biomedical imaging. The PF-SDM compactly encodes geometric and topological properties of closed shapes, including their skeleton and symmetries. This provides robust and interpretable features for shape comparison and machine learning. The PF-SDM is mathematically smooth, providing access to gradients and differential-geometric quantities. It also extends to temporal dynamics and allows fusing spatial intensity distributions, such as genetic markers, with shape dynamics. We present the PF-SDM theory, benchmark it on synthetic data, and apply it to predicting body-axis formation in mouse gastruloids, outperforming a CNN baseline in both accuracy and speed.

翻译：我们提出了推前向符号距离形态计量学（PF-SDM），用于生物医学成像中的形状量化。PF-SDM紧凑地编码了封闭形状的几何与拓扑特性，包括其骨架与对称性，为形状比较与机器学习提供了稳健且可解释的特征。该方法在数学上是光滑的，可支持梯度与微分几何量的计算。它还可扩展至时间动态分析，并允许将空间强度分布（如遗传标记）与形状动态融合。我们阐述了PF-SDM的理论框架，在合成数据上进行了基准测试，并将其应用于预测小鼠胃胚体的体轴形成过程，在准确性与速度上均优于基于CNN的基线方法。