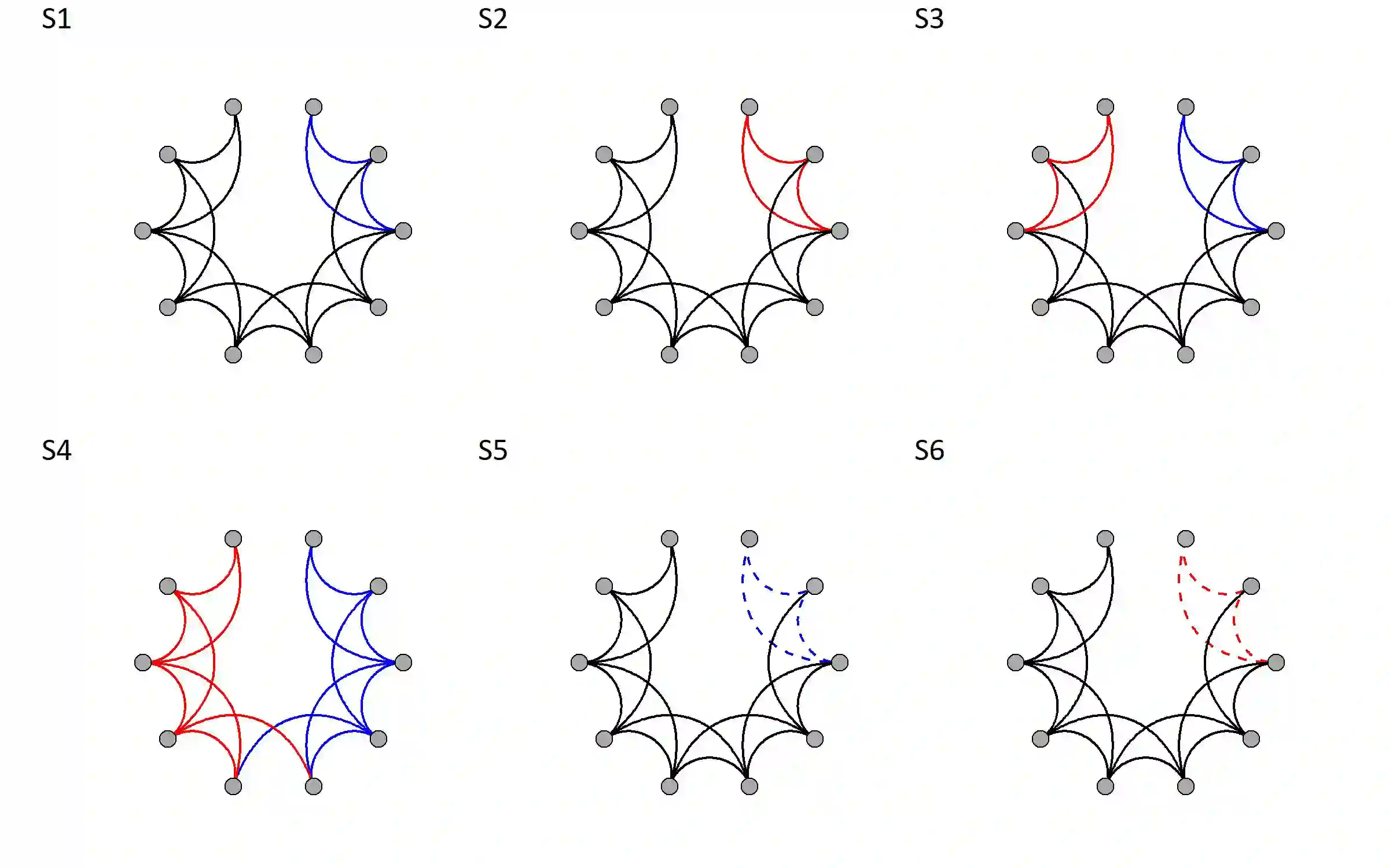
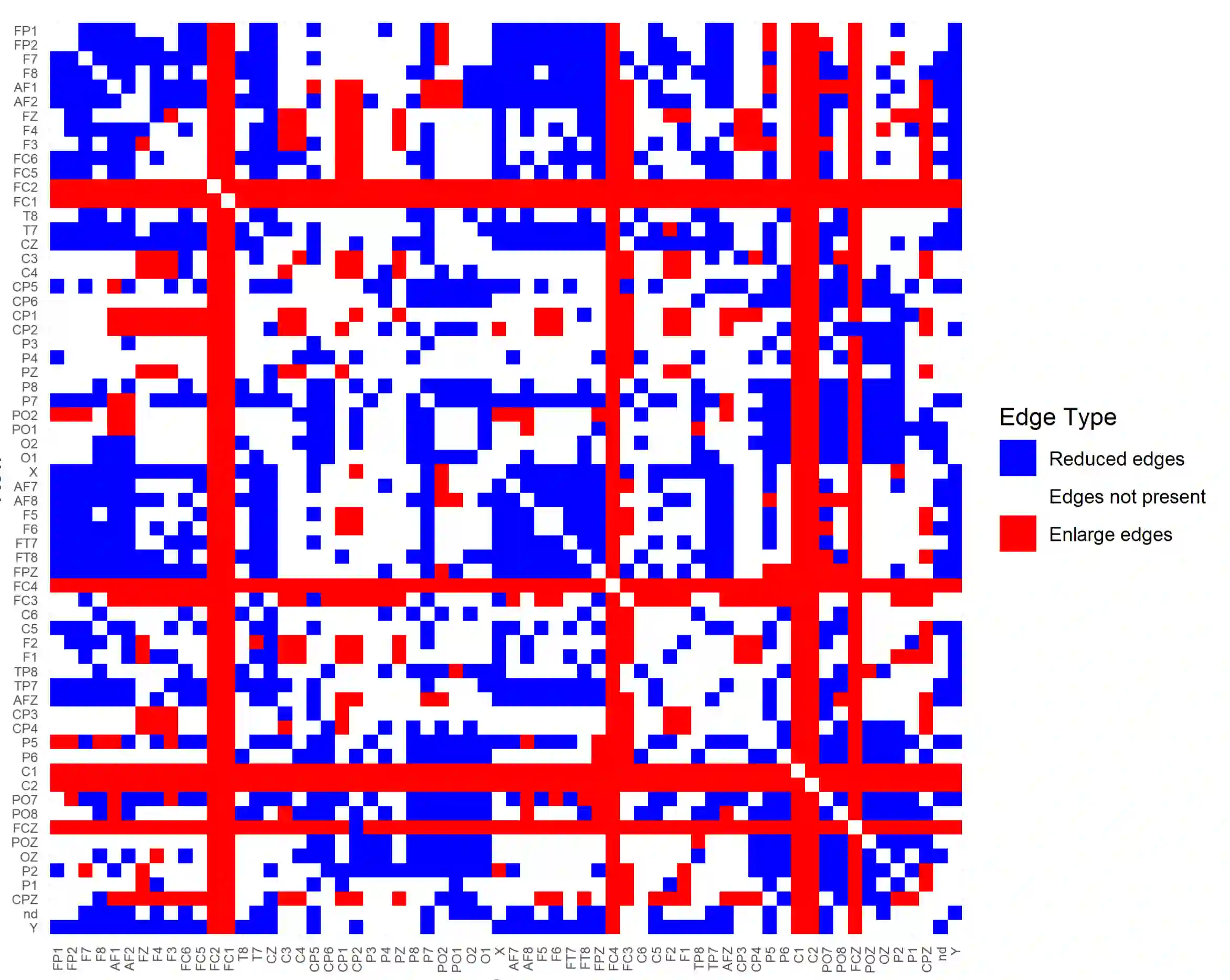
Estimation of brain functional connectivity from EEG data is of great importance both for medical research and diagnosis. It involves quantifying the conditional dependencies among the activity of different brain areas from the time-varying electric field recorded by sensors placed outside the scalp. These dependencies may vary within and across individuals and be influenced by covariates such as age, mental status, or disease severity. Motivated by this problem, we propose a novel neighbour selection approach based on functional-on-functional regression for the characterization of conditional Gaussian functional graphical models. We provide a fully automated, data-driven procedure for inferring conditional dependence structures among observed functional variables. In particular, pairwise interactions are directly identified and allowed to vary as a function of covariates, enabling covariate-specific modulation of connectivity patterns. Our proposed method accommodates an arbitrary number of continuous and discrete covariates. Moreover, unlike existing methods for direct estimation of differential graphical models, the proposed approach yields directly interpretable coefficients, allowing discrimination between covariate-induced increases and decreases in interaction strength. The methodology is evaluated through extensive simulation studies and an application to experimental EEG data. The results demonstrate clear advantages over existing approaches, including higher estimation accuracy and substantially reduced computational cost, especially in high-dimensional settings.

翻译：从脑电图数据中估计大脑功能连接性对于医学研究和诊断具有重要意义。这涉及根据头皮外部传感器记录到的时变电场，量化不同脑区活动之间的条件依赖性。这些依赖性可能在个体内部和个体之间存在差异，并受到年龄、精神状态或疾病严重程度等协变量的影响。受此问题启发，我们提出了一种基于函数对函数回归的新型邻域选择方法，用于刻画条件高斯函数图模型。我们提供了一种全自动、数据驱动的程序，用于推断观测函数变量之间的条件依赖结构。特别地，该方法直接识别成对交互作用，并允许其随协变量变化，从而实现对连接模式的协变量特异性调控。我们提出的方法能够容纳任意数量的连续和离散协变量。此外，与现有直接估计差异图模型的方法不同，所提方法能够直接产生可解释的系数，从而可以区分由协变量引起的交互强度增加和减少。该方法通过广泛的模拟研究和实验脑电图数据应用进行了评估。结果表明，相较于现有方法，该方法具有明显优势，包括更高的估计精度和显著降低的计算成本，尤其是在高维设置下。