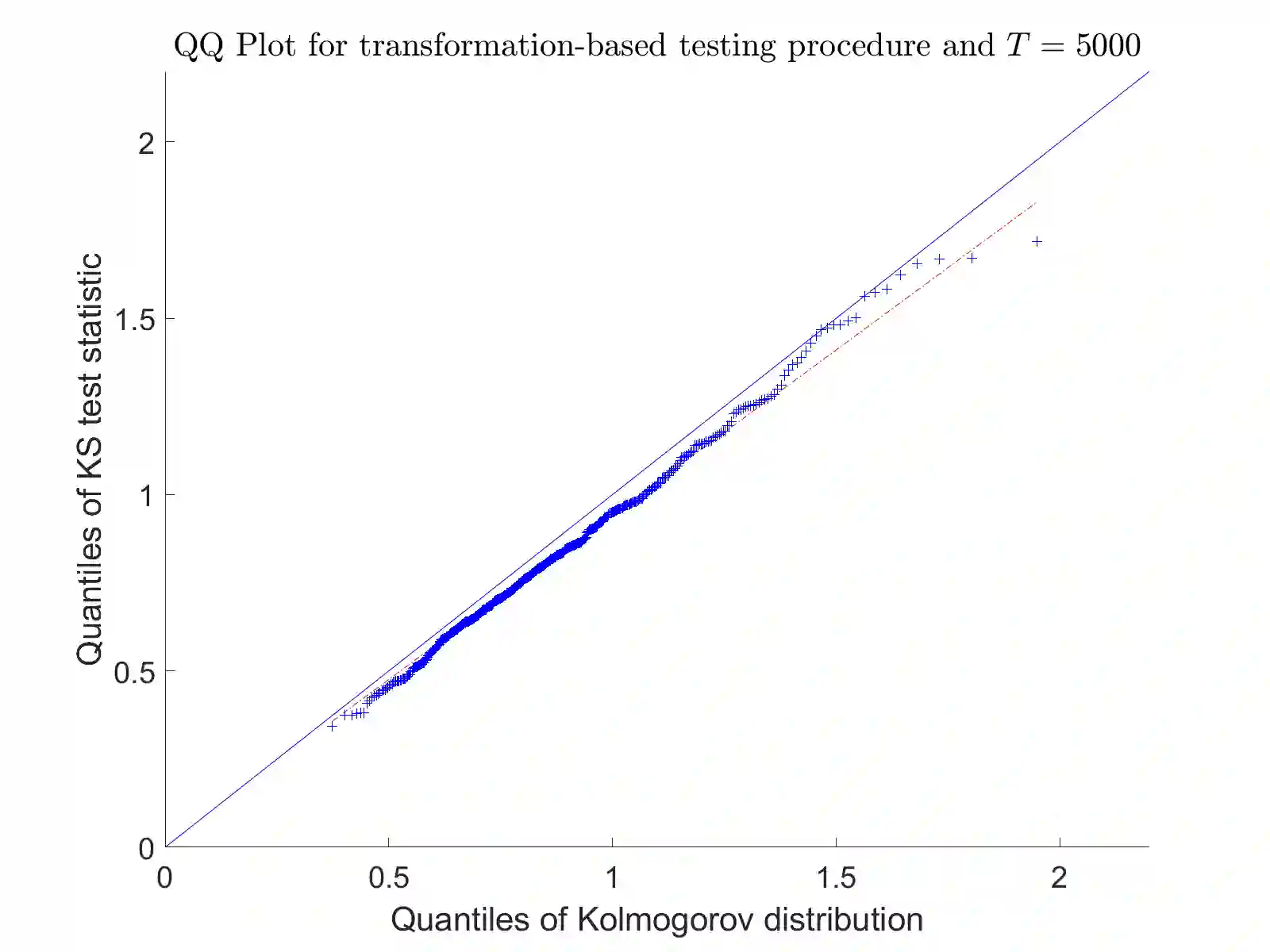
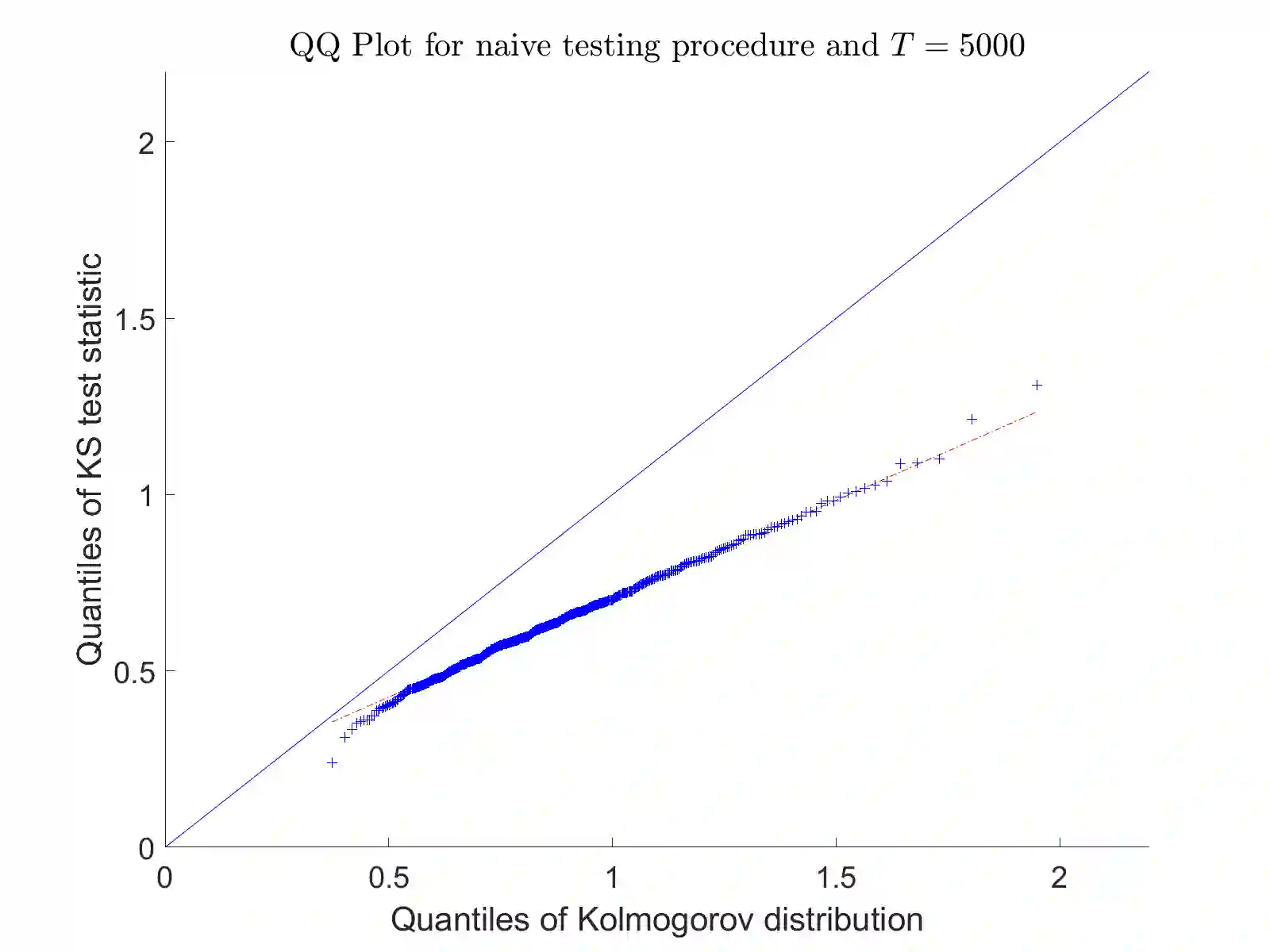
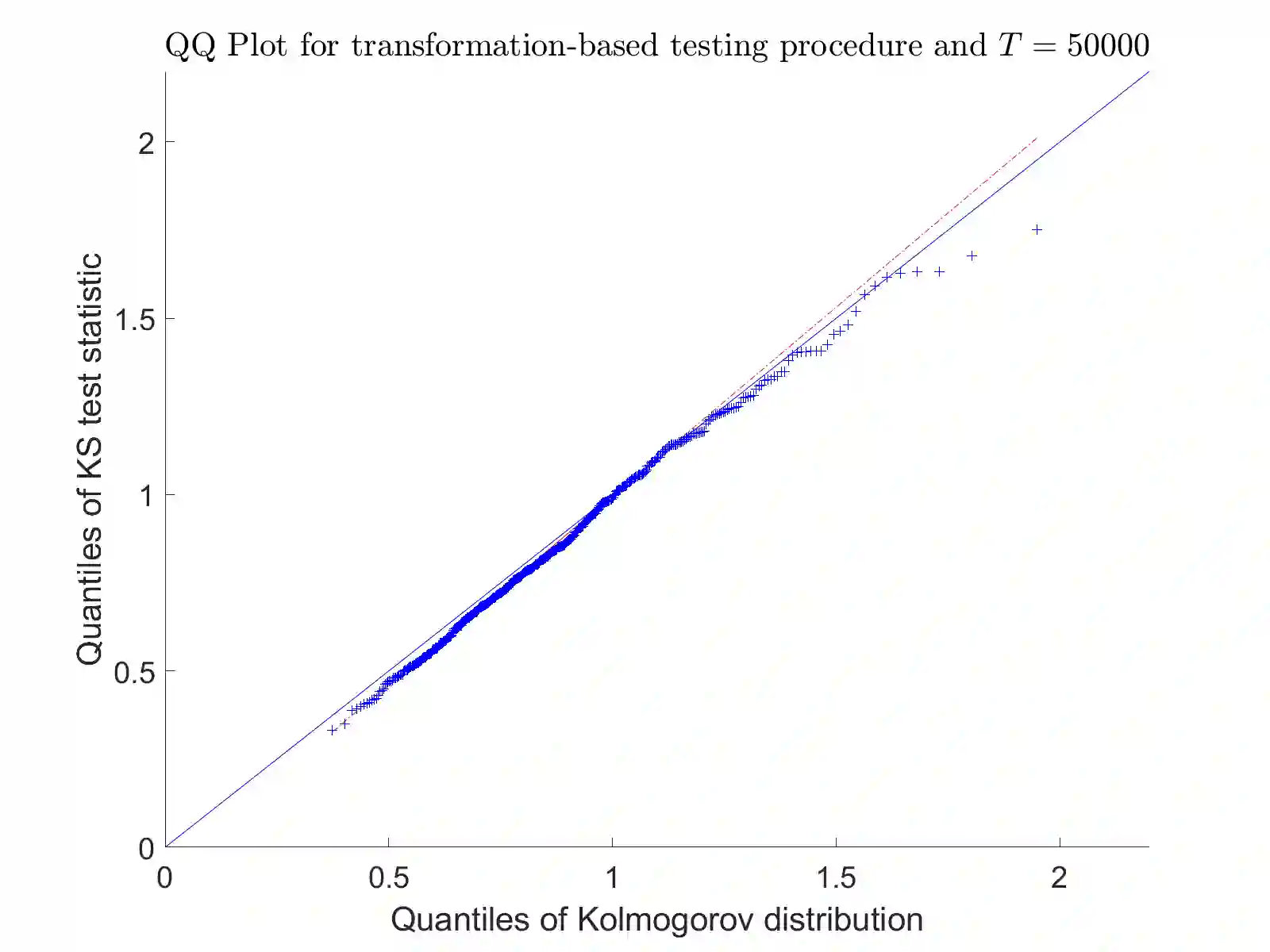
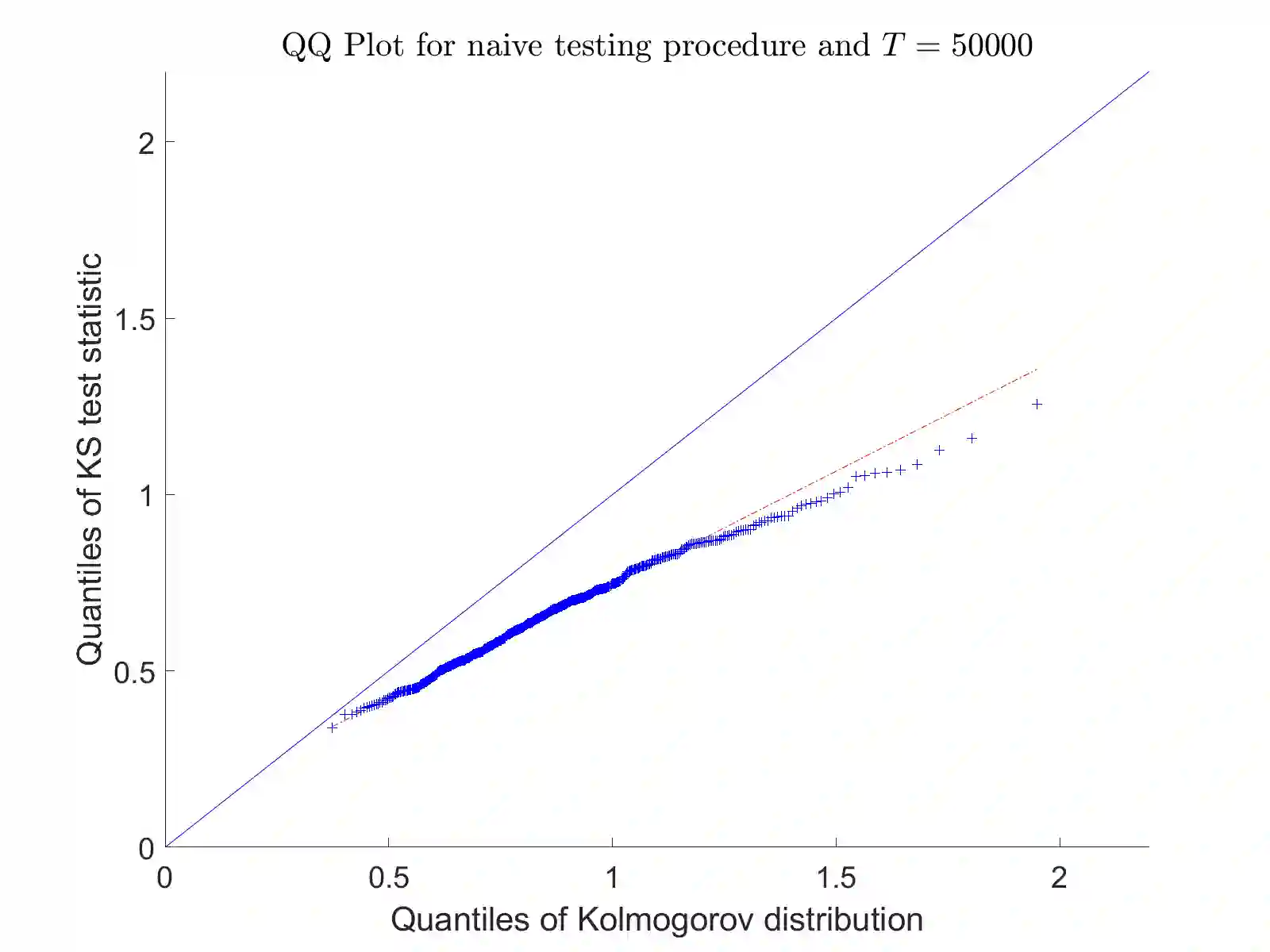
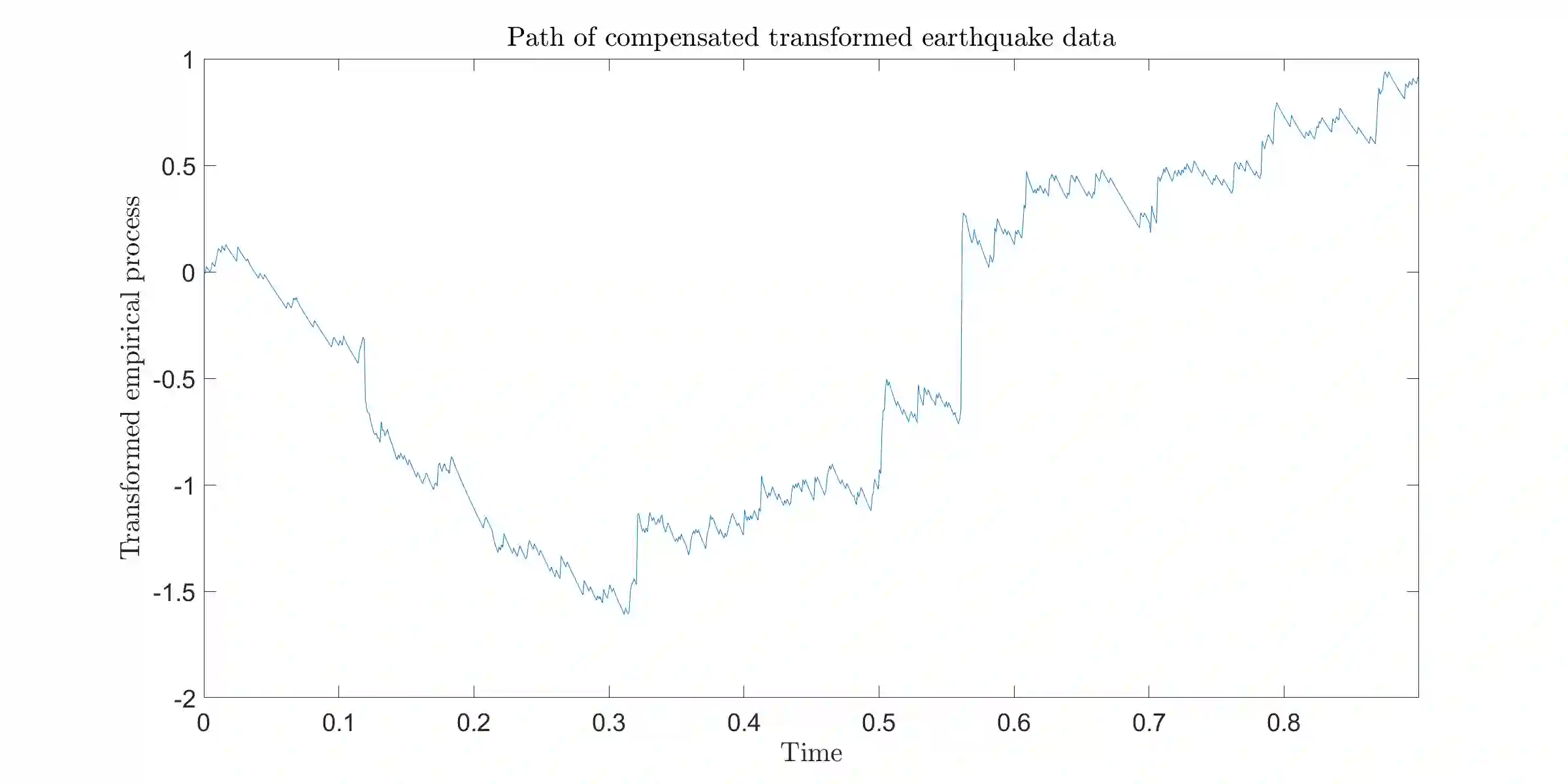
Consider an observation of a multivariate temporal point process $N$ with law $\mathcal P$ on the time interval $[0,T]$. To test the null hypothesis that $\mathcal P$ belongs to a given parametric family, we construct a convergent compensated counting process to which we apply an innovation martingale transformation. We prove that the resulting process converges weakly to a standard Wiener process. Consequently, taking a suitable functional of this process yields an asymptotically distribution-free goodness-of-fit test for point processes. For several standard tests based on the increments of this transformed process, we establish consistency under alternative hypotheses. Finally, we assess the performance of the proposed testing procedure through a Monte Carlo simulation study and illustrate its practical utility with two real-data examples.

翻译：考虑在时间区间$[0,T]$上观测到一个具有分布$\mathcal P$的多元时间点过程$N$。为检验$\mathcal P$属于给定参数族这一原假设，我们构造了一个收敛的补偿计数过程，并对其应用创新鞅变换。我们证明了所得过程弱收敛于标准维纳过程。因此，选取该过程的适当泛函可得到渐近分布自由的点过程拟合优度检验。针对基于该变换过程增量的若干标准检验，我们建立了备择假设下的一致性。最后，通过蒙特卡洛模拟研究评估了所提检验程序的性能，并利用两个实际数据案例说明了其实际效用。