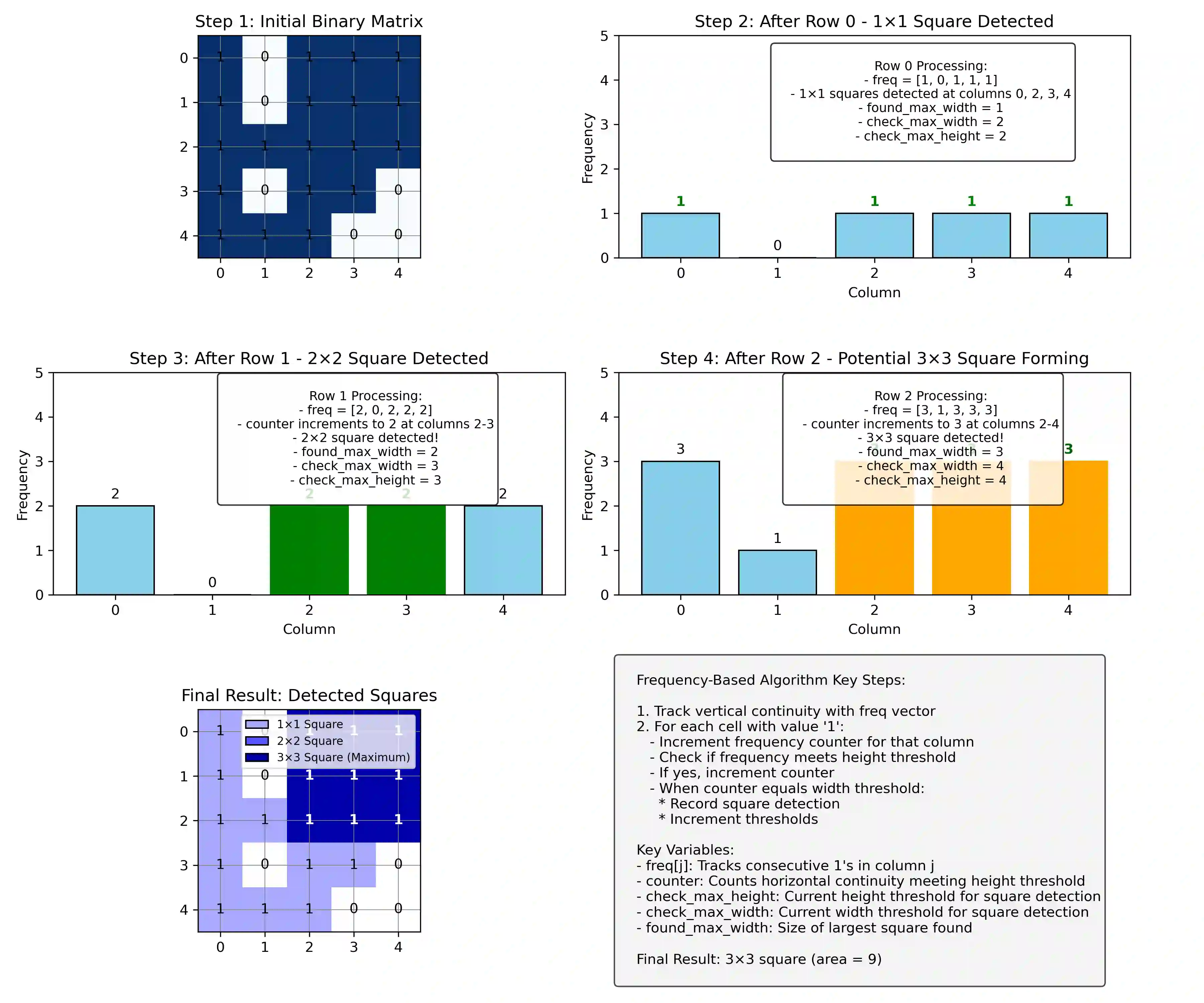
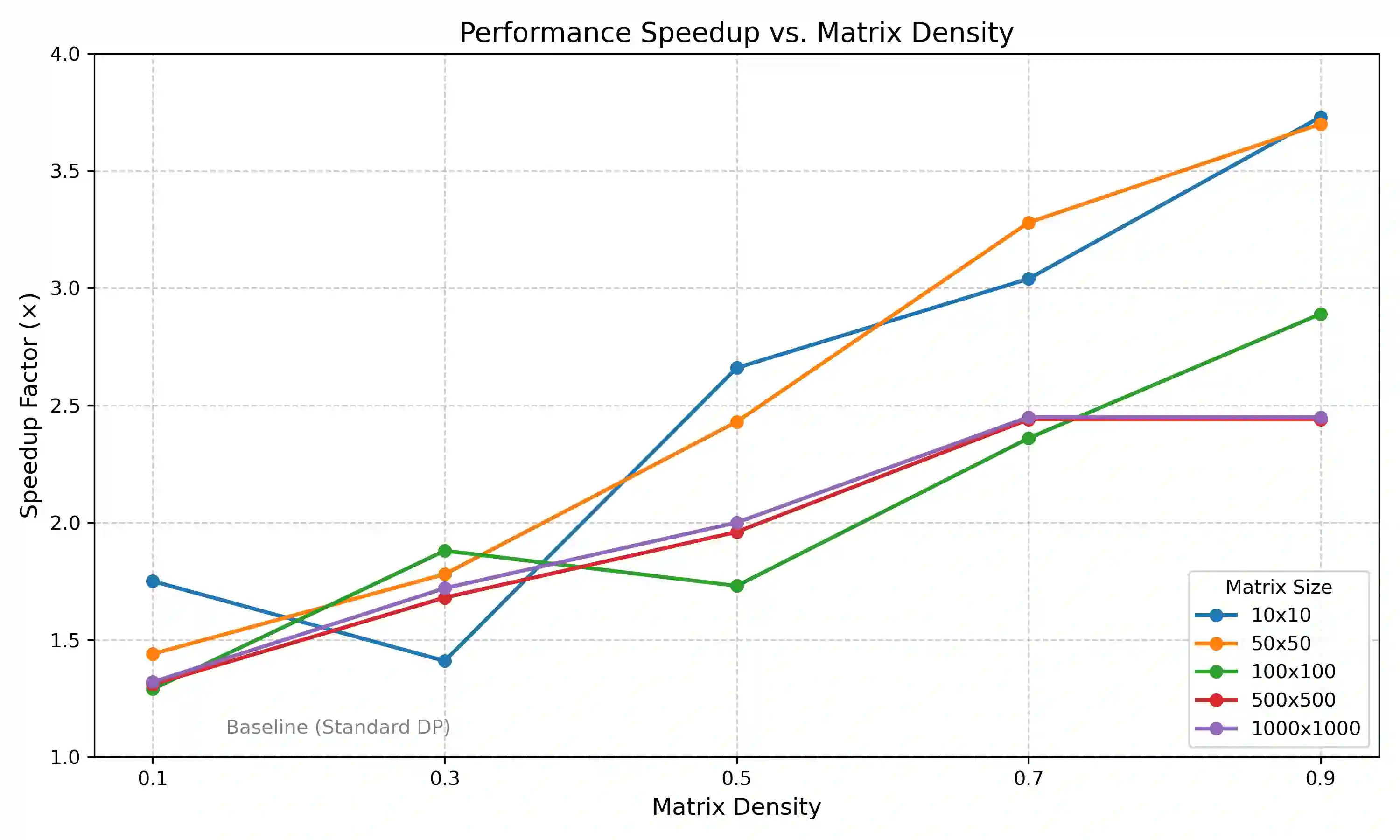
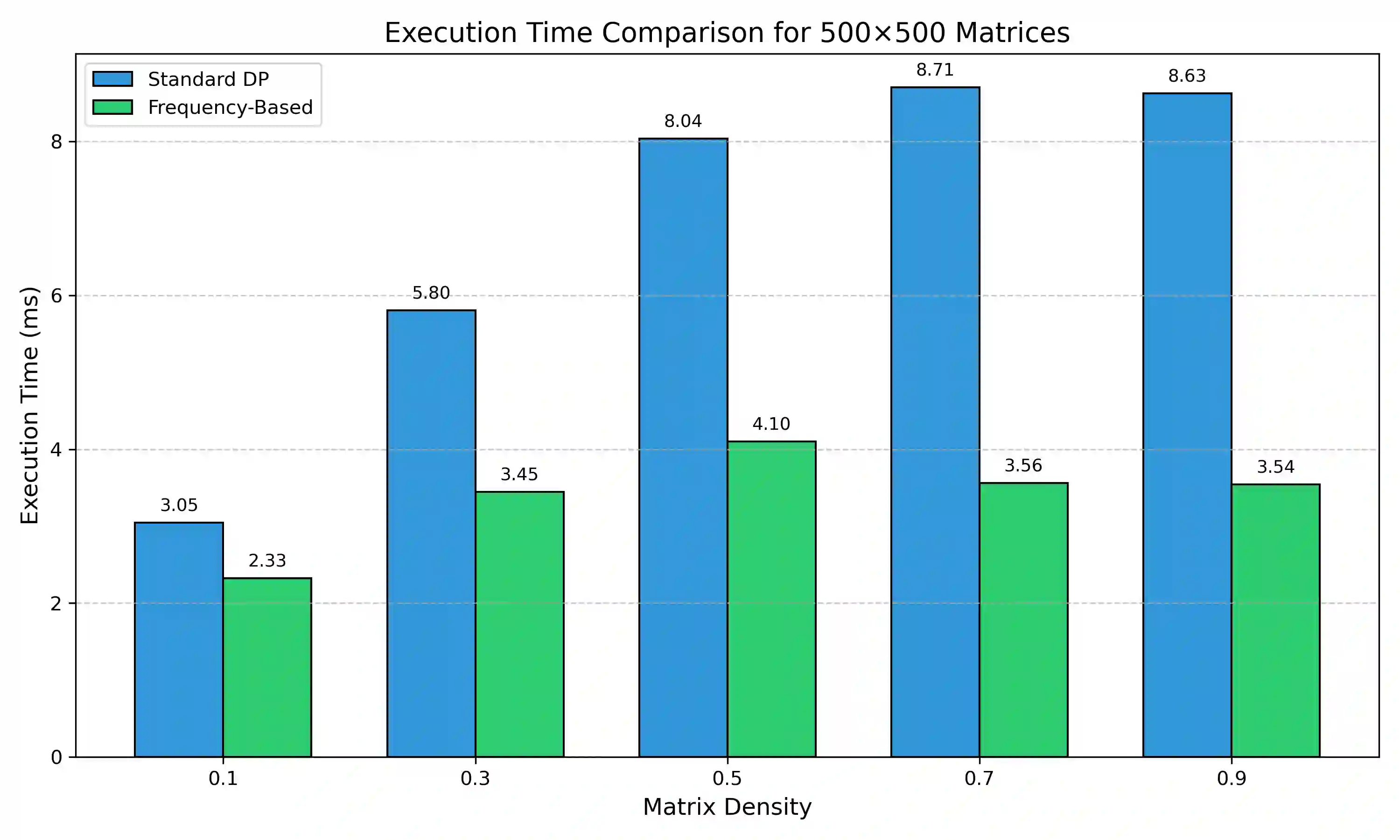
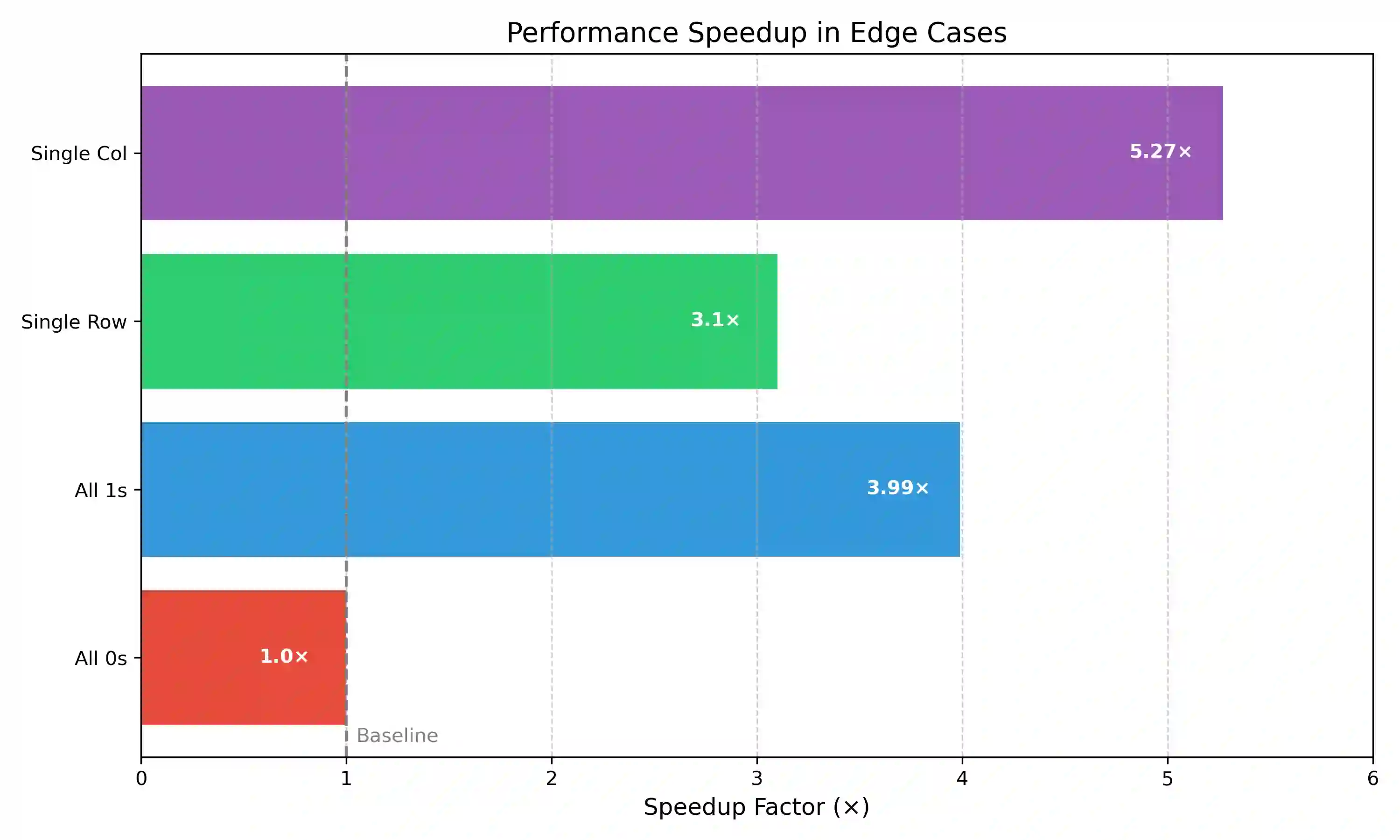
This paper presents a novel frequency-based algorithm which solves the maximal square problem with improved practical speed performance while maintaining optimal asymptotic complexity. My approach tracks the columnar continuity of ones through an adaptive frequency vector and dynamic thresholding mechanism that eliminates the need for nested minimum operations commonly found in standard dynamic programming solutions. Theoretical analysis confirms a time complexity of O(mn) and a space complexity of O(n).Formal loop-invariant proofs verify correctness, while comprehensive benchmarking demonstrates speed improvements of 1.3-5x over standard methods in various matrix densities and sizes. This method improves algorithm design and simultaneously creates opportunities for faster spatial pattern recognition in fields like urban planning, environmental science, and medical imaging.

翻译：本文提出了一种新颖的基于频率的算法，该算法在保持最优渐近复杂度的同时，以改进的实际速度性能解决了最大正方形问题。该方法通过自适应频率向量和动态阈值机制跟踪“1”的列连续性，从而消除了标准动态规划解决方案中常见的嵌套最小值运算需求。理论分析证实了时间复杂度为O(mn)和空间复杂度为O(n)。形式化的循环不变式证明验证了其正确性，而全面的基准测试表明，在不同矩阵密度和大小下，其速度比标准方法提高了1.3至5倍。该方法不仅改进了算法设计，同时为城市规划、环境科学和医学成像等领域的空间模式识别创造了更快的处理机会。