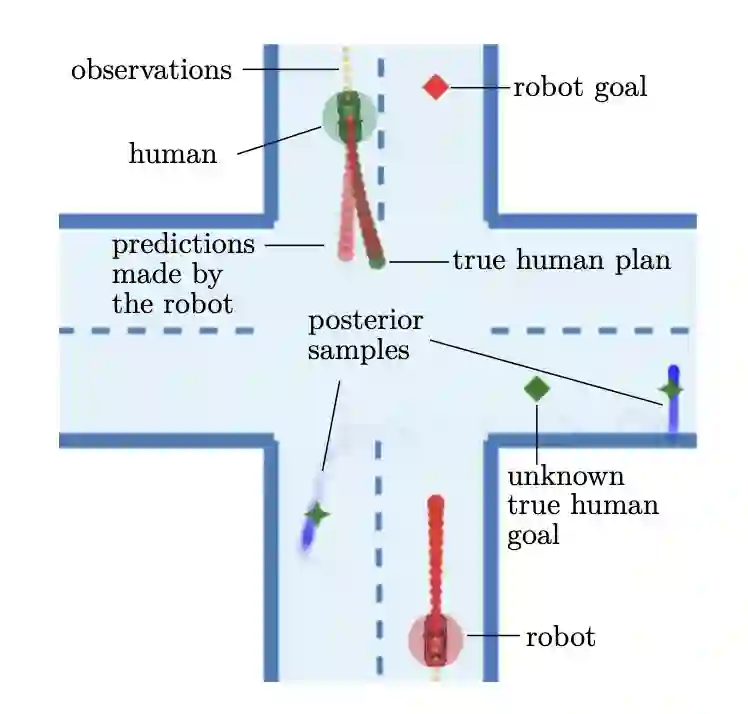
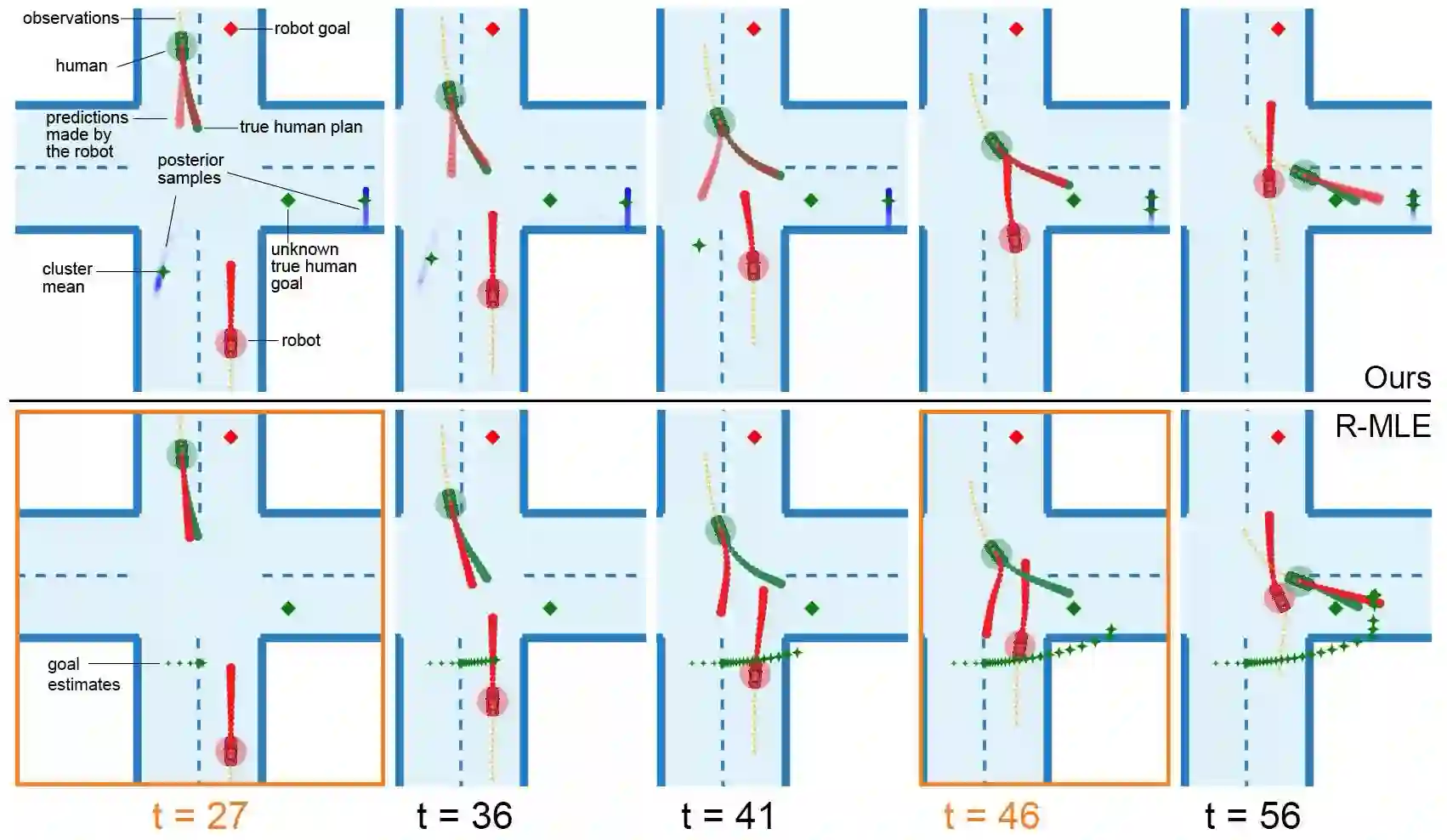
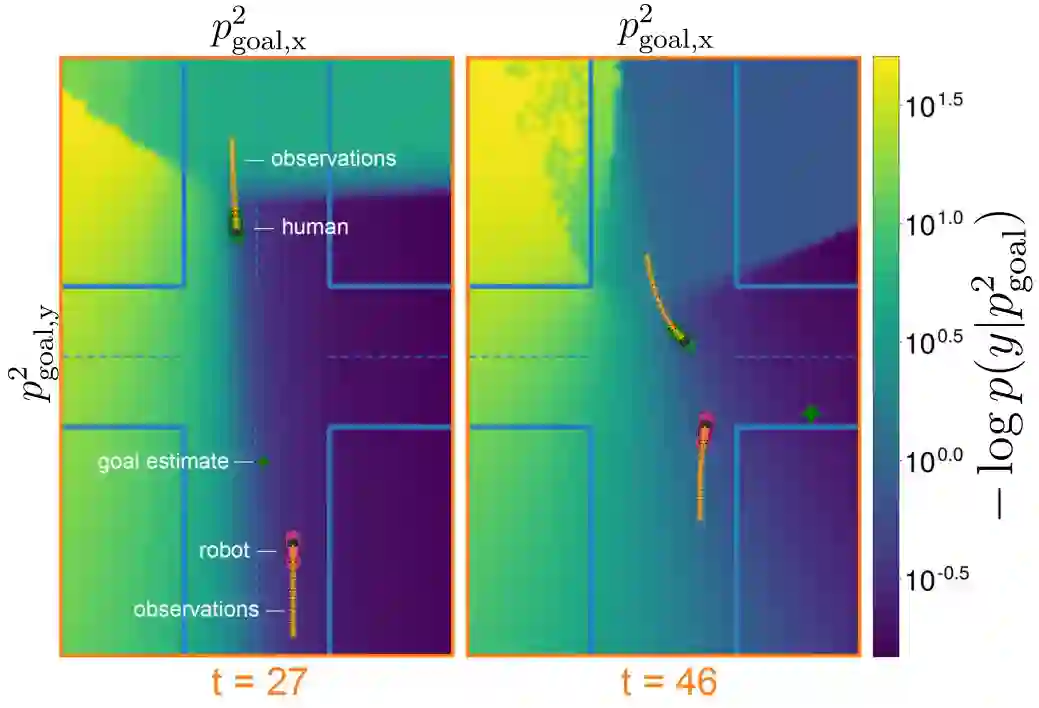
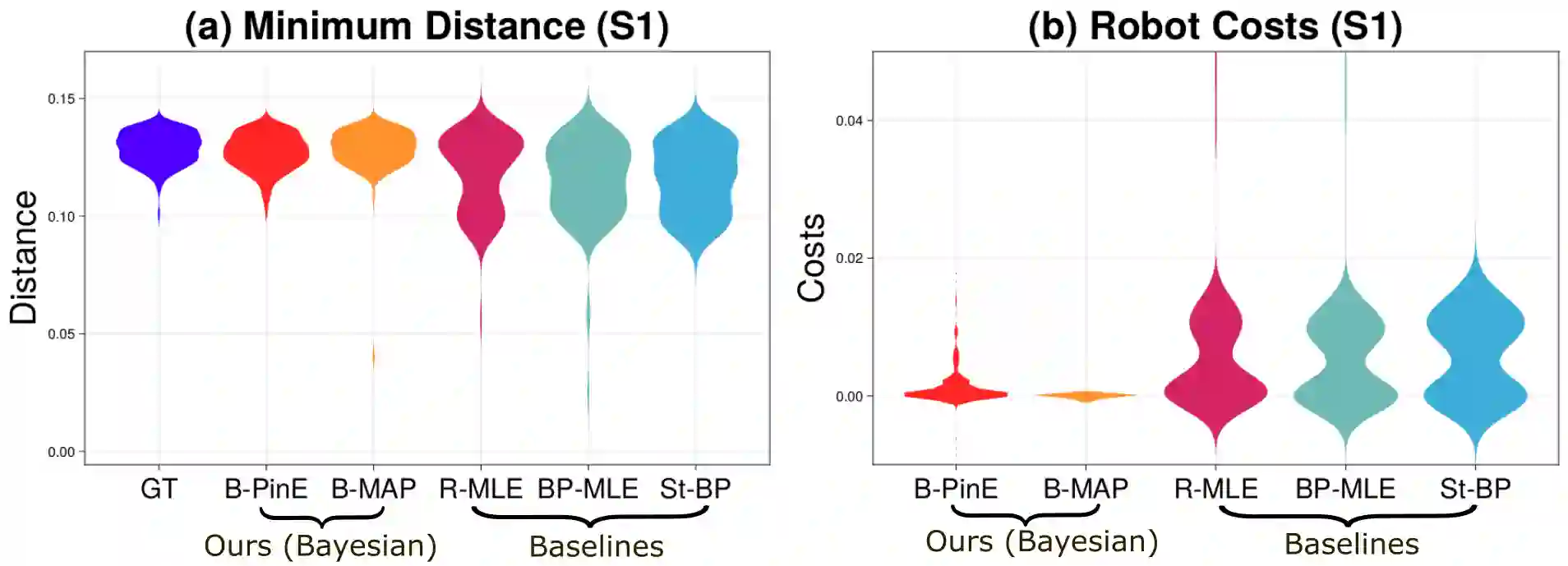
Many multi-agent interaction scenarios can be naturally modeled as noncooperative games, where each agent's decisions depend on others' future actions. However, deploying game-theoretic planners for autonomous decision-making requires a specification of all agents' objectives. To circumvent this practical difficulty, recent work develops maximum likelihood techniques for solving inverse games that can identify unknown agent objectives from interaction data. Unfortunately, these methods only infer point estimates and do not quantify estimator uncertainty; correspondingly, downstream planning decisions can overconfidently commit to unsafe actions. We present an approximate Bayesian inference approach for solving the inverse game problem, which can incorporate observation data from multiple modalities and be used to generate samples from the Bayesian posterior over the hidden agent objectives given limited sensor observations in real time. Concretely, the proposed Bayesian inverse game framework trains a structured variational autoencoder with an embedded differentiable Nash game solver on interaction datasets and does not require labels of agents' true objectives. Extensive experiments show that our framework successfully learns prior and posterior distributions, improves inference quality over maximum likelihood estimation-based inverse game approaches, and enables safer downstream decision-making without sacrificing efficiency. When trajectory information is uninformative or unavailable, multimodal inference further reduces uncertainty by exploiting additional observation modalities.

翻译：许多多智能体交互场景可自然地建模为非合作博弈，其中每个智能体的决策均依赖于其他智能体的未来行为。然而，为自主决策部署博弈论规划器需要明确所有智能体的目标函数。为规避这一实际困难，近期研究发展了基于最大似然估计的逆博弈求解技术，能够从交互数据中识别未知的智能体目标。遗憾的是，这些方法仅能推断点估计值，无法量化估计器的不确定性；相应地，下游规划决策可能因过度自信而采取不安全行动。本文提出一种近似贝叶斯推断方法用于求解逆博弈问题，该方法能够融合多模态观测数据，并可在给定有限实时传感器观测的条件下，从隐藏智能体目标的贝叶斯后验分布中生成样本。具体而言，所提出的贝叶斯逆博弈框架在交互数据集上训练具有嵌入式可微分纳什博弈求解器的结构化变分自编码器，且无需标注智能体的真实目标函数。大量实验表明，我们的框架成功学习了先验与后验分布，相比基于最大似然估计的逆博弈方法提升了推断质量，并在保持效率的同时实现了更安全的下游决策。当轨迹信息不具信息性或不可获取时，多模态推断通过利用额外观测模态进一步降低了不确定性。