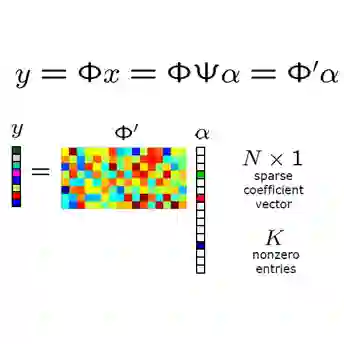
In compressed sensing (CS), sparse signals can be reconstructed from significantly fewer samples than required by the Nyquist-Shannon sampling theorem. While non-sparse signals can be sparsely represented in appropriate transformation domains, conventional CS frameworks rely on the incoherence of the measurement matrix columns to guarantee reconstruction performance. This paper proposes a novel method termed Dimension-Keeping Semi-Tensor Product Compressed Sensing (DK-STP-CS), which leverages intra-group correlations while maintaining inter-group incoherence to enhance the measurement matrix design. Specifically, the DK-STP algorithm is integrated into the design of the sensing matrix, enabling dimensionality reduction while preserving signal recovery capability. For image compression and reconstruction tasks, the proposed method achieves notable noise suppression and improves visual fidelity. Experimental results demonstrate that DK-STP-CS significantly outperforms traditional CS and STP-CS approaches, as evidenced by higher Peak Signal-to-Noise Ratio (PSNR) values between the reconstructed and original images. The robustness of DK-STP-CS is further validated under noisy conditions and varying sampling rates, highlighting its potential for practical applications in resource-constrained environments.

翻译：在压缩感知(CS)中，稀疏信号可以从远少于奈奎斯特-香农采样定理要求的样本中重构。虽然非稀疏信号可以在适当的变换域中稀疏表示，但传统CS框架依赖于测量矩阵列的非相干性来保证重构性能。本文提出了一种称为保持维度的半张量积压缩感知(DK-STP-CS)的新方法，该方法在保持组间非相干性的同时利用组内相关性来增强测量矩阵设计。具体而言，将DK-STP算法集成到感知矩阵设计中，在保持信号恢复能力的同时实现降维。对于图像压缩和重构任务，所提方法实现了显著的噪声抑制并提高了视觉保真度。实验结果表明，DK-STP-CS显著优于传统CS和STP-CS方法，重构图像与原始图像之间更高的峰值信噪比(PSNR)值证明了这一点。DK-STP-CS的鲁棒性在噪声条件和不同采样率下得到进一步验证，突显了其在资源受限环境中实际应用的潜力。