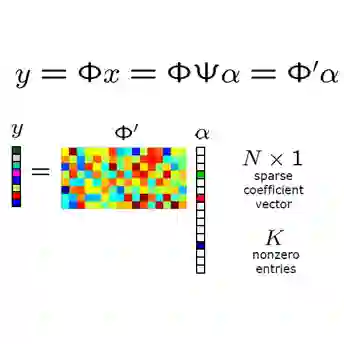
In the set reconciliation (\textsf{SetR}) problem, two parties Alice and Bob, holding sets $\mathsf{A}$ and $\mathsf{B}$, communicate to learn the symmetric difference $\mathsf{A} \Delta \mathsf{B}$. In this work, we study a related but under-explored problem: set intersection (\textsf{SetX})~\cite{Ozisik2019}, where both parties learn $\mathsf{A} \cap \mathsf{B}$ instead. However, existing solutions typically reuse \textsf{SetR} protocols due to the absence of dedicated \textsf{SetX} protocols and the misconception that \textsf{SetR} and \textsf{SetX} have comparable costs. Observing that \textsf{SetX} is fundamentally cheaper than \textsf{SetR}, we developed a multi-round \textsf{SetX} protocol that outperforms the information-theoretic lower bound of \textsf{SetR} problem. In our \textsf{SetX} protocol, Alice sends Bob a compressed sensing (CS) sketch of $\mathsf{A}$ to help Bob identify his unique elements (those in $\mathsf{B \setminus A}$). This solves the \textsf{SetX} problem, if $\mathsf{A} \subseteq \mathsf{B}$. Otherwise, Bob sends a CS sketch of the residue (a set of elements he cannot decode) back to Alice for her to decode her unique elements (those in $\mathsf{A \setminus B}$). As such, Alice and Bob communicate back and forth %with a set membership filter (SMF) of estimated $\mathsf{B \setminus A}$. Alice updates $\mathsf{A}$ and communication repeats until both parties agrees on $\mathsf{A} \cap \mathsf{B}$. On real world datasets, experiments show that our $\mathsf{SetX}$ protocol reduces the communication cost by 8 to 10 times compared to the IBLT-based $\mathsf{SetR}$ protocol.

翻译：在集合协调（SetR）问题中，持有集合 $\mathsf{A}$ 和 $\mathsf{B}$ 的两方 Alice 与 Bob 通过通信来获知对称差 $\mathsf{A} \Delta \mathsf{B}$。本文研究一个相关但尚未被充分探索的问题：集合交集（SetX）~\cite{Ozisik2019}，即双方学习 $\mathsf{A} \cap \mathsf{B}$。然而，由于缺乏专用的 SetX 协议以及认为 SetR 与 SetX 成本相当的误解，现有解决方案通常复用 SetR 协议。我们观察到 SetX 本质上比 SetR 成本更低，因此开发了一种多轮 SetX 协议，其性能超越了 SetR 问题的信息论下界。在我们的 SetX 协议中，Alice 向 Bob 发送 $\mathsf{A}$ 的压缩感知（CS）草图，以帮助 Bob 识别其独有的元素（即 $\mathsf{B \setminus A}$ 中的元素）。若 $\mathsf{A} \subseteq \mathsf{B}$，此过程即解决了 SetX 问题。否则，Bob 将残差（一组他无法解码的元素）的 CS 草图发回给 Alice，以便 Alice 解码其独有的元素（即 $\mathsf{A \setminus B}$ 中的元素）。如此，Alice 与 Bob 交替通信 %并利用估计的 $\mathsf{B \setminus A}$ 的集合成员过滤器（SMF）。Alice 更新 $\mathsf{A}$ 并重复通信，直至双方就 $\mathsf{A} \cap \mathsf{B}$ 达成一致。在真实世界数据集上的实验表明，与基于 IBLT 的 SetR 协议相比，我们的 $\mathsf{SetX}$ 协议将通信成本降低了 8 至 10 倍。