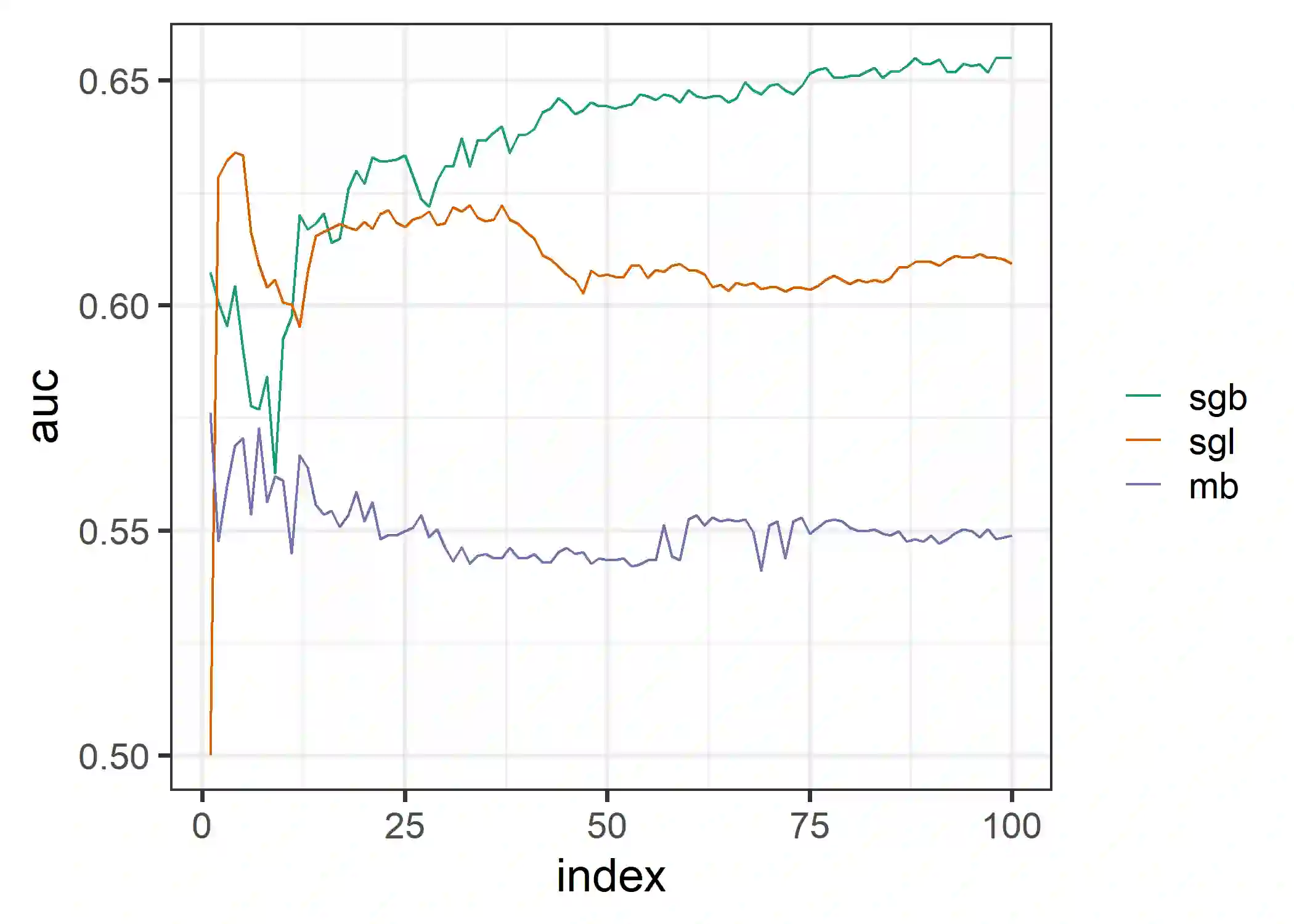
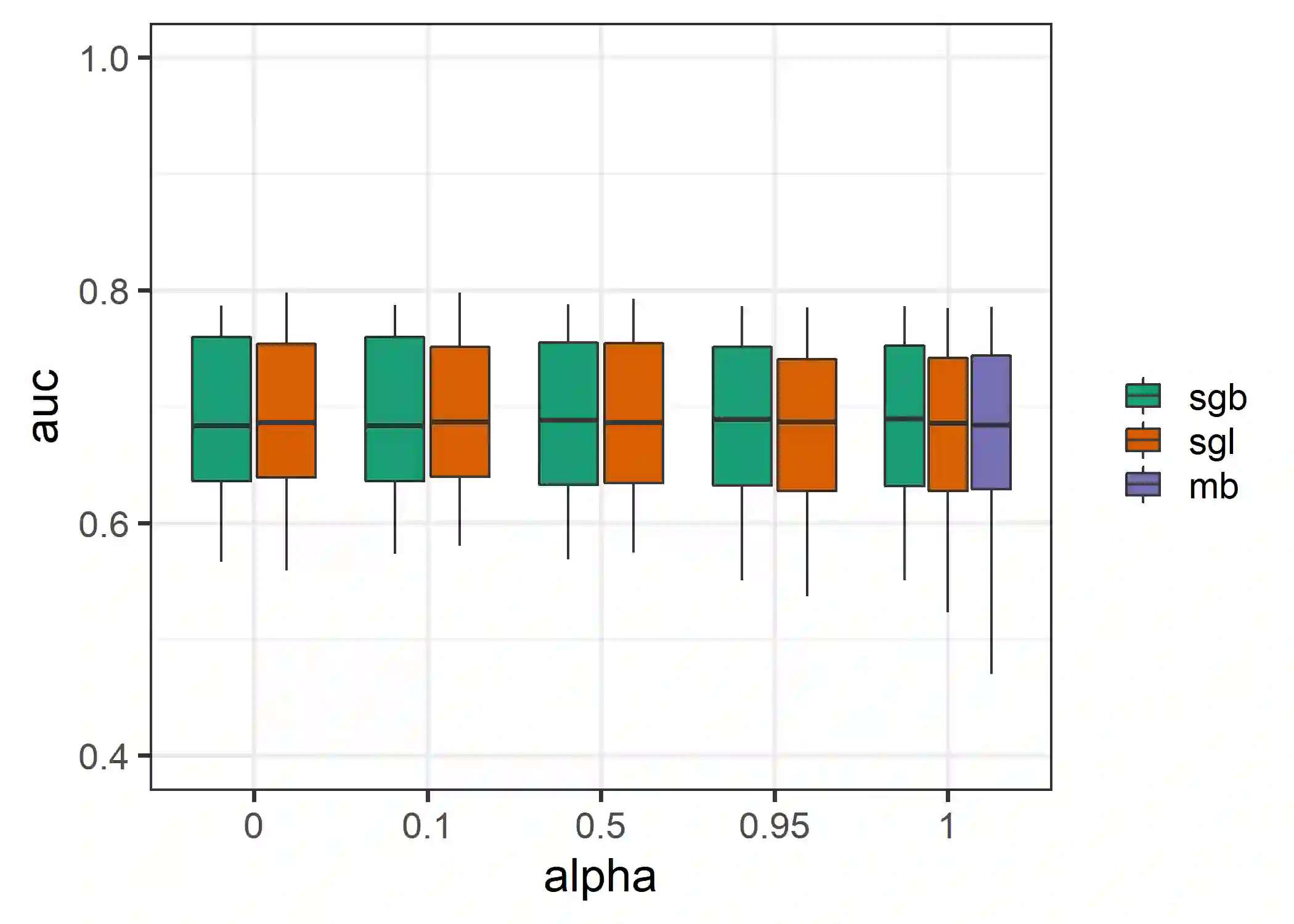
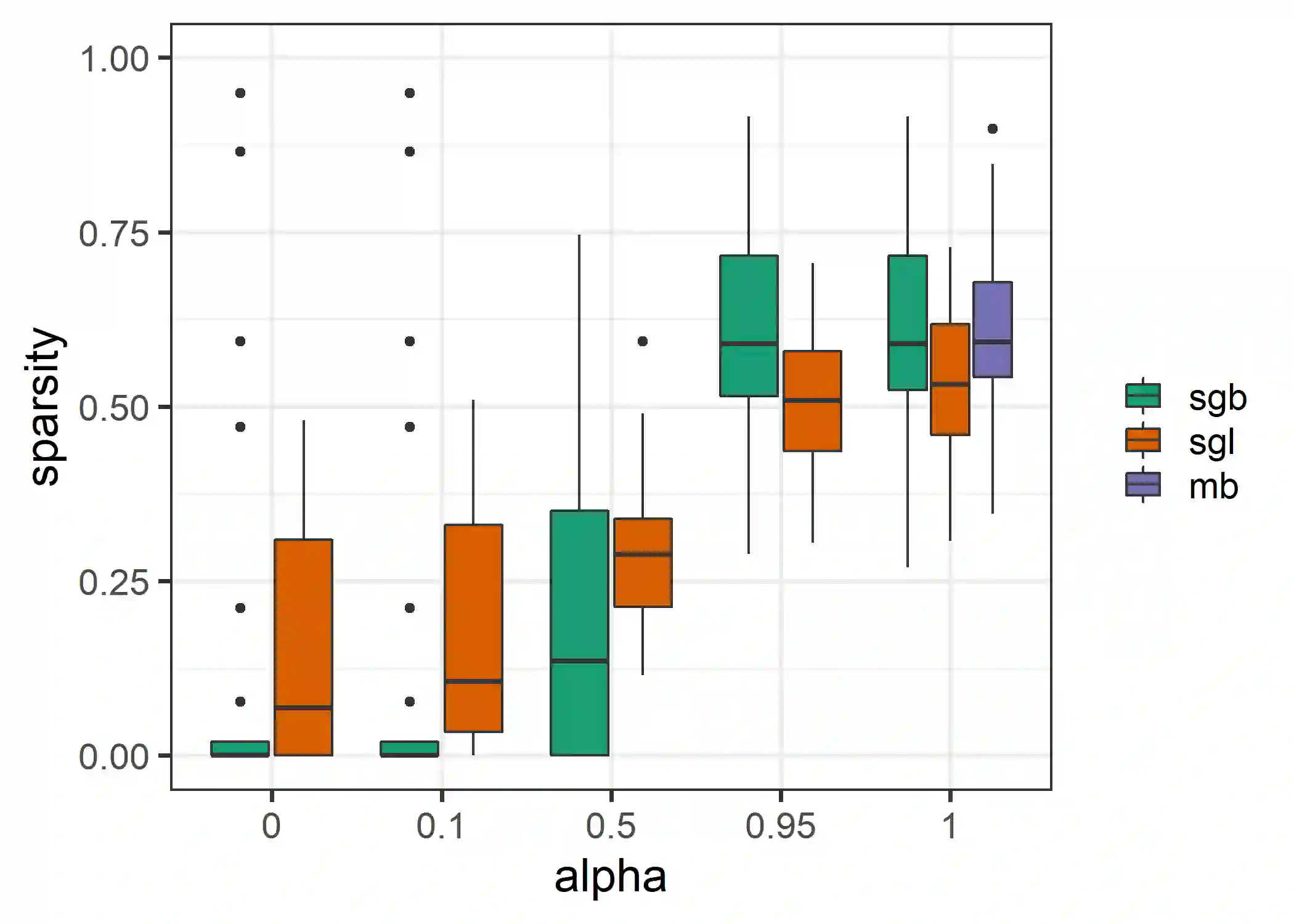
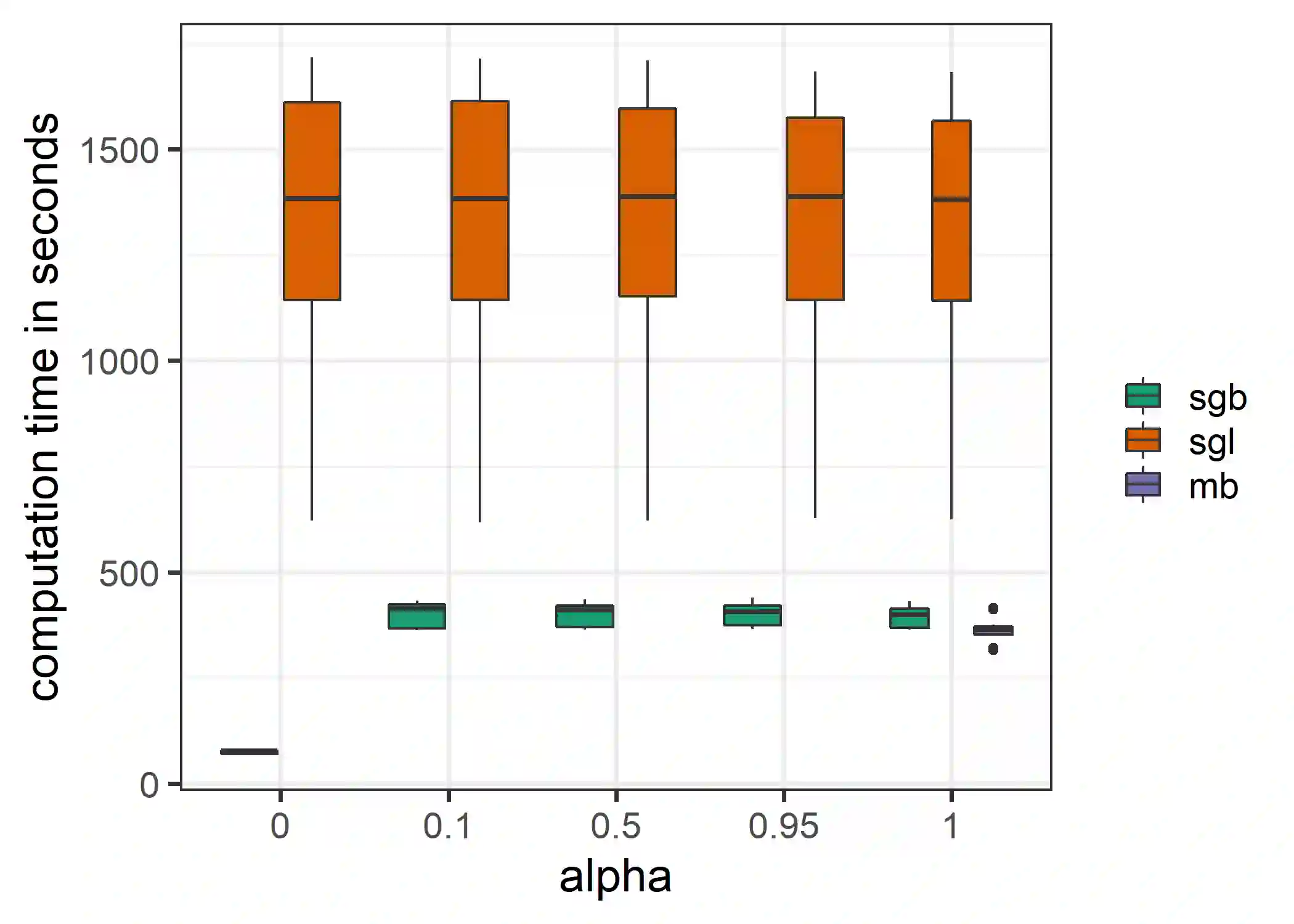
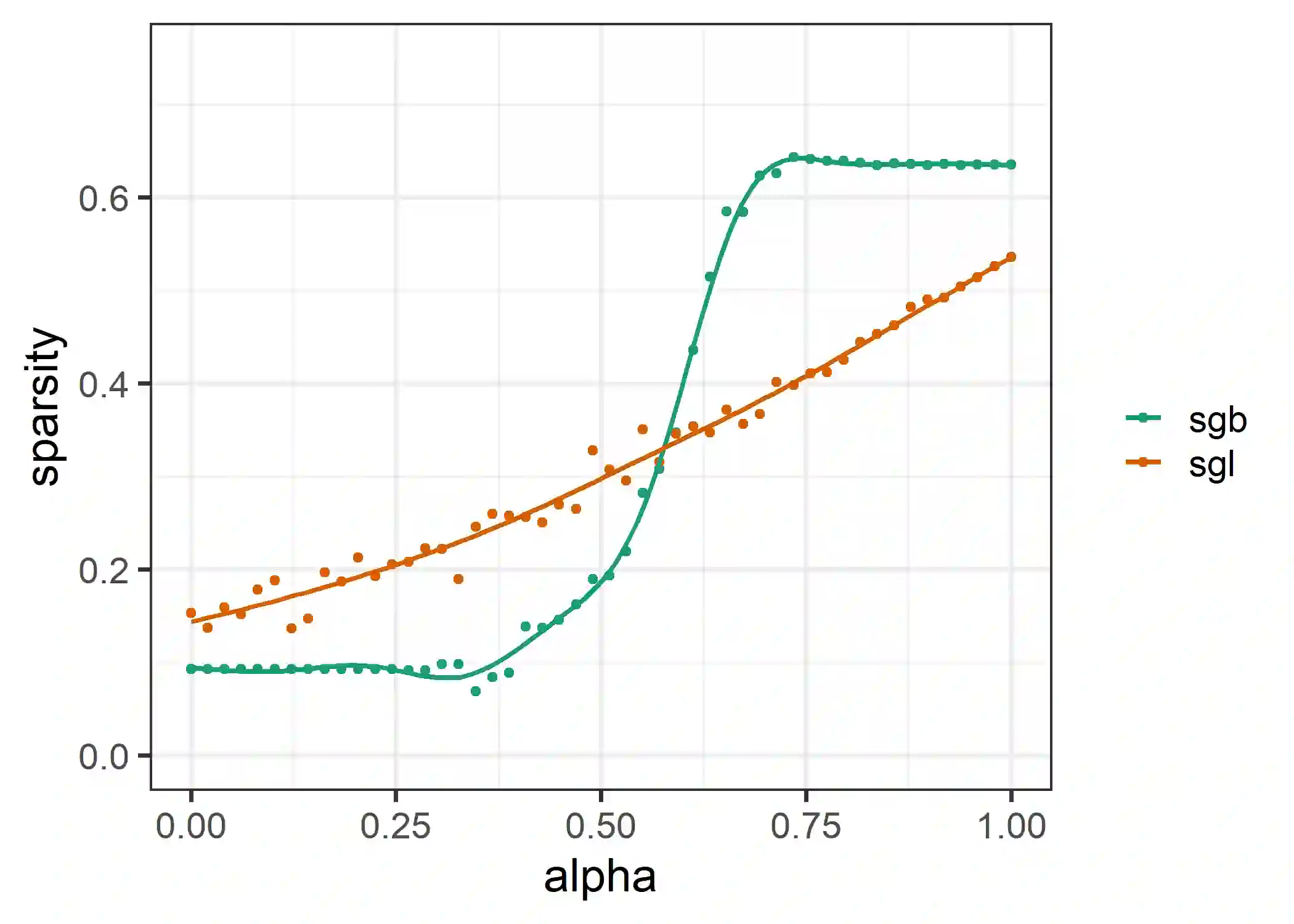
In the presence of grouped covariates, we propose a framework for boosting that allows to enforce sparsity within and between groups. By using component-wise and group-wise gradient boosting at the same time with adjusted degrees of freedom, a model with similar properties as the sparse group lasso can be fitted through boosting. We show that within-group and between-group sparsity can be controlled by a mixing parameter and discuss similarities and differences to the mixing parameter in the sparse group lasso. With simulations, gene data as well as agricultural data we show the effectiveness and predictive competitiveness of this estimator. The data and simulations suggest, that in the presence of grouped variables the use of sparse group boosting is associated with less biased variable selection and higher predictability compared to component-wise boosting. Additionally, we propose a way of reducing bias in component-wise boosting through the degrees of freedom.

翻译：在组群共变的情况下,我们提出一个提振框架,以强制各组内部和群体之间的宽度。通过使用组件和群度梯度,同时与调整自由度同时进行推升,可以通过提振来安装一个与稀少组群长相类似的模型。我们表明,组内和组间宽度可以通过混合参数加以控制,并讨论与稀少组群的混合参数的异同之处。通过模拟、基因数据以及农业数据,我们显示了这个估测器的有效性和预测竞争力。数据和模拟表明,在组群变量存在的情况下,利用稀有组群推动与组分推力相比,与偏差的变异选择和更高的可预测性有关。此外,我们建议了一种方法,通过自由度减少成份推进中的偏差。