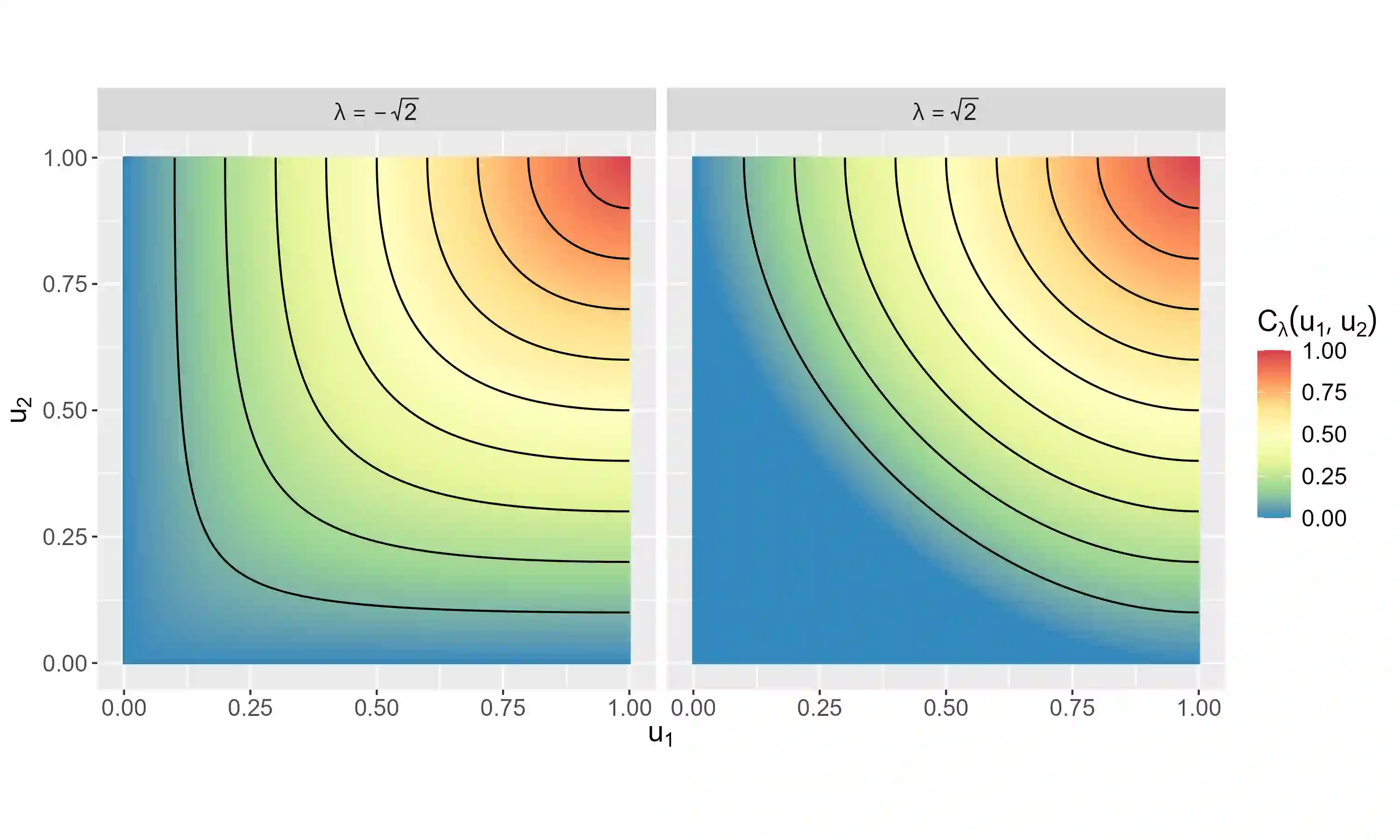
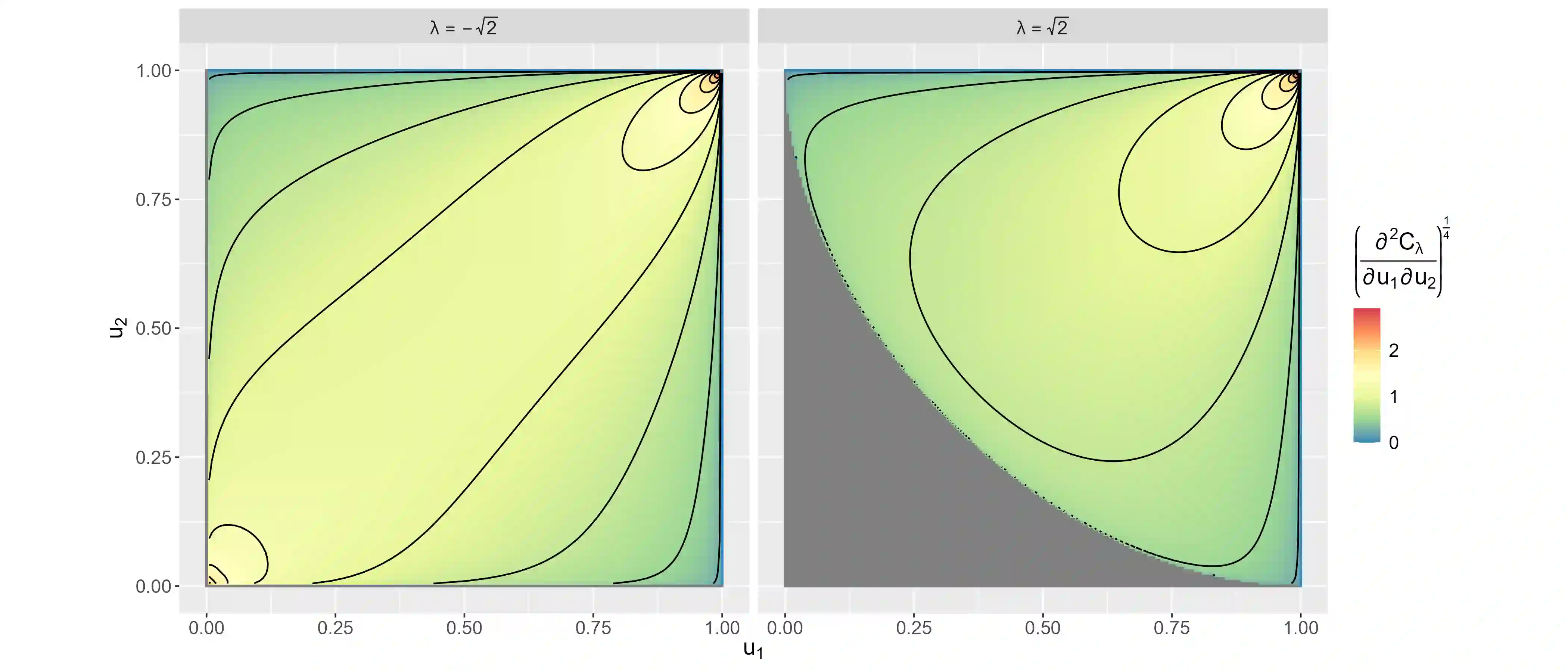
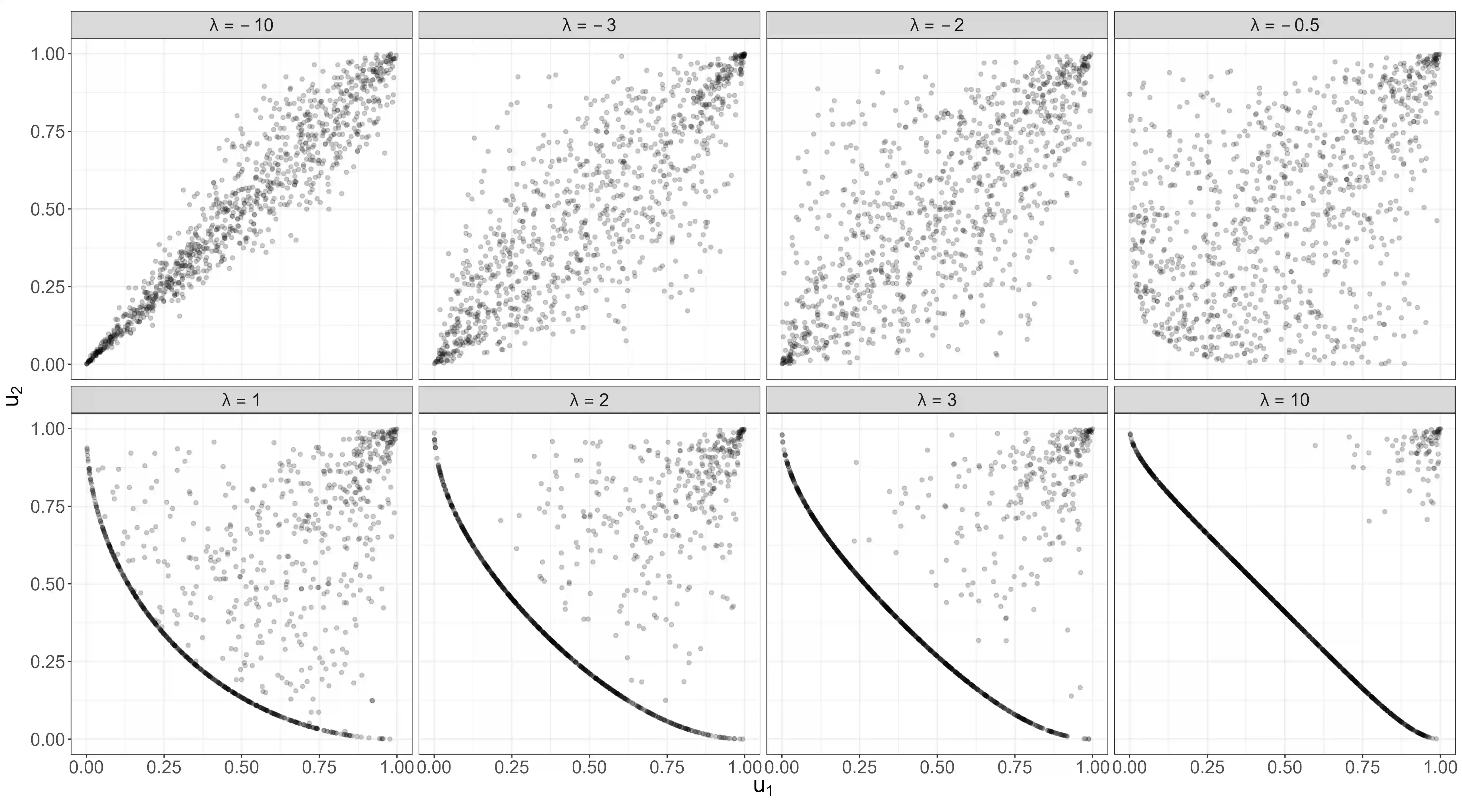
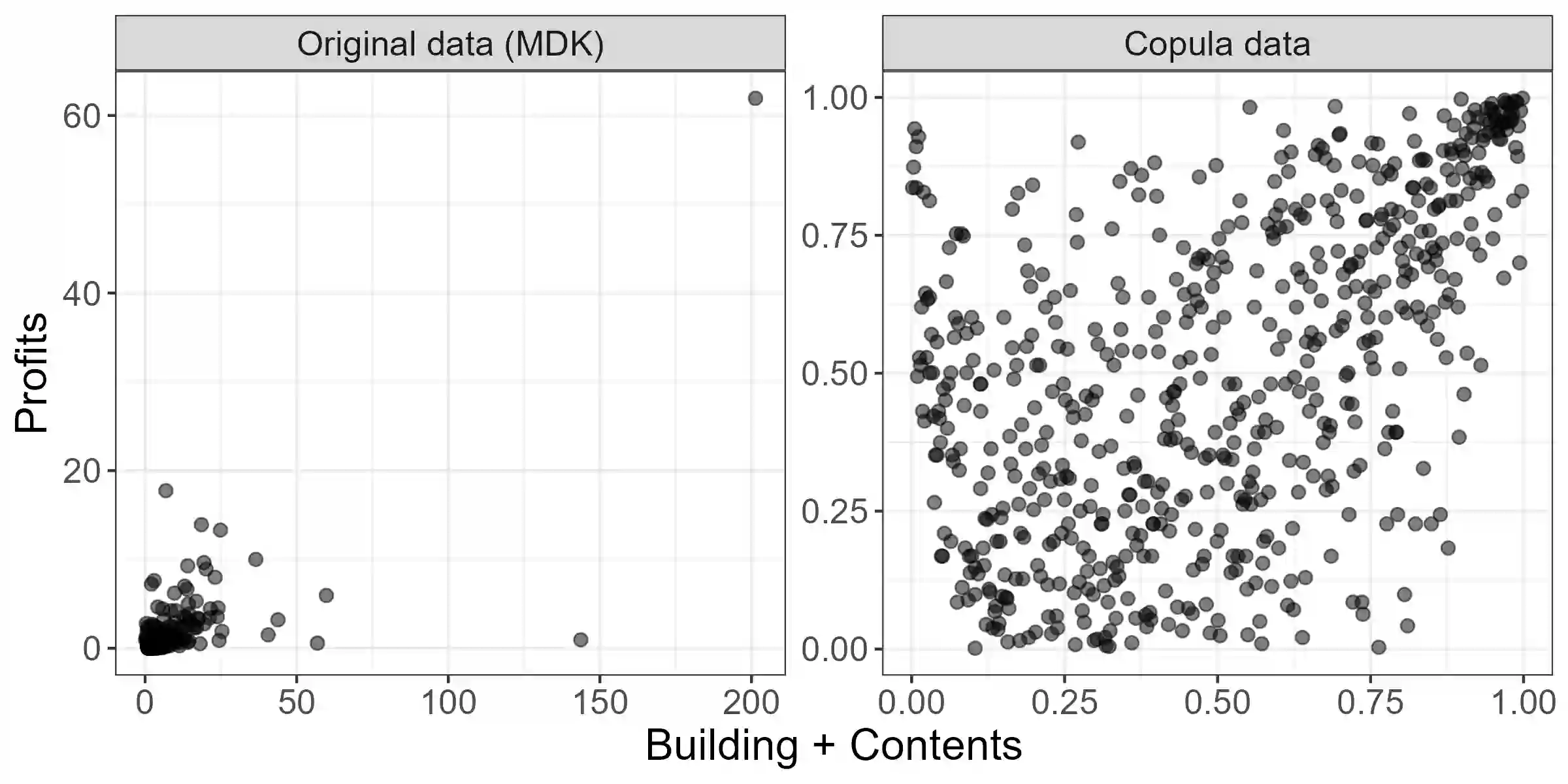
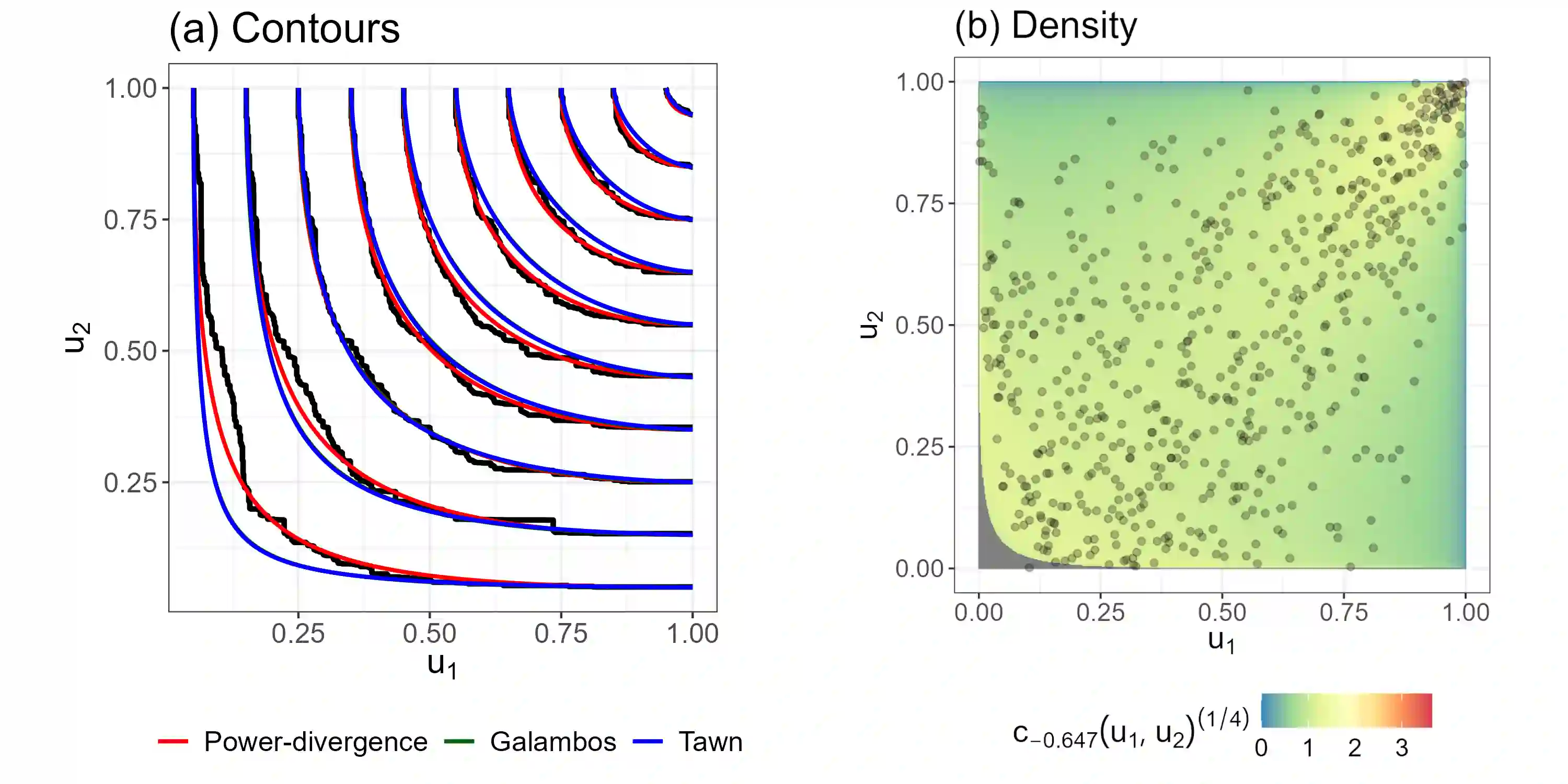
This paper demonstrates that, under a particular convention, the convex functions that characterise the phi divergences also generate Archimedean copulas in at least two dimensions. As a special case, we develop the family of Archimedean copulas associated with the important family of power divergences, which we call the power-divergence copulas. The properties of the family are extensively studied, including the subfamilies that are absolutely continuous or have a singular component, the ordering of the family, limiting cases (i.e., the Frechet-Hoeffding lower bound and Frechet-Hoeffding upper bound), the Kendall's tau and tail-dependence coefficients, and cases that extend to three or more dimensions. In an illustrative application, the power-divergence copulas are used to model a Danish fire insurance dataset. It is shown that the power-divergence copulas provide an adequate fit to the bivariate distribution of two kinds of fire-related losses claimed by businesses, while several benchmarks (a suite of well known Archimedean, extreme-value, and elliptical copulas) do not.

翻译：本文证明，在特定约定下，表征φ散度的凸函数也能生成至少二维的阿基米德连接函数。作为特例，我们构建了与重要的幂散度族相关联的阿基米德连接函数族，称之为幂散度连接函数。我们对该函数族的性质进行了全面研究，包括其绝对连续或含奇异分量的子族、族内排序、极限情形（即弗雷歇-霍夫丁下界与上界）、肯德尔τ系数与尾部相依系数，以及向三维及以上维度的扩展情形。在示例应用中，幂散度连接函数被用于建模丹麦火灾保险数据集。研究表明，幂散度连接函数能充分拟合企业申报的两种火灾相关损失的双变量分布，而若干基准模型（包括一系列知名的阿基米德连接函数、极值连接函数和椭圆连接函数）则未能实现这一拟合效果。