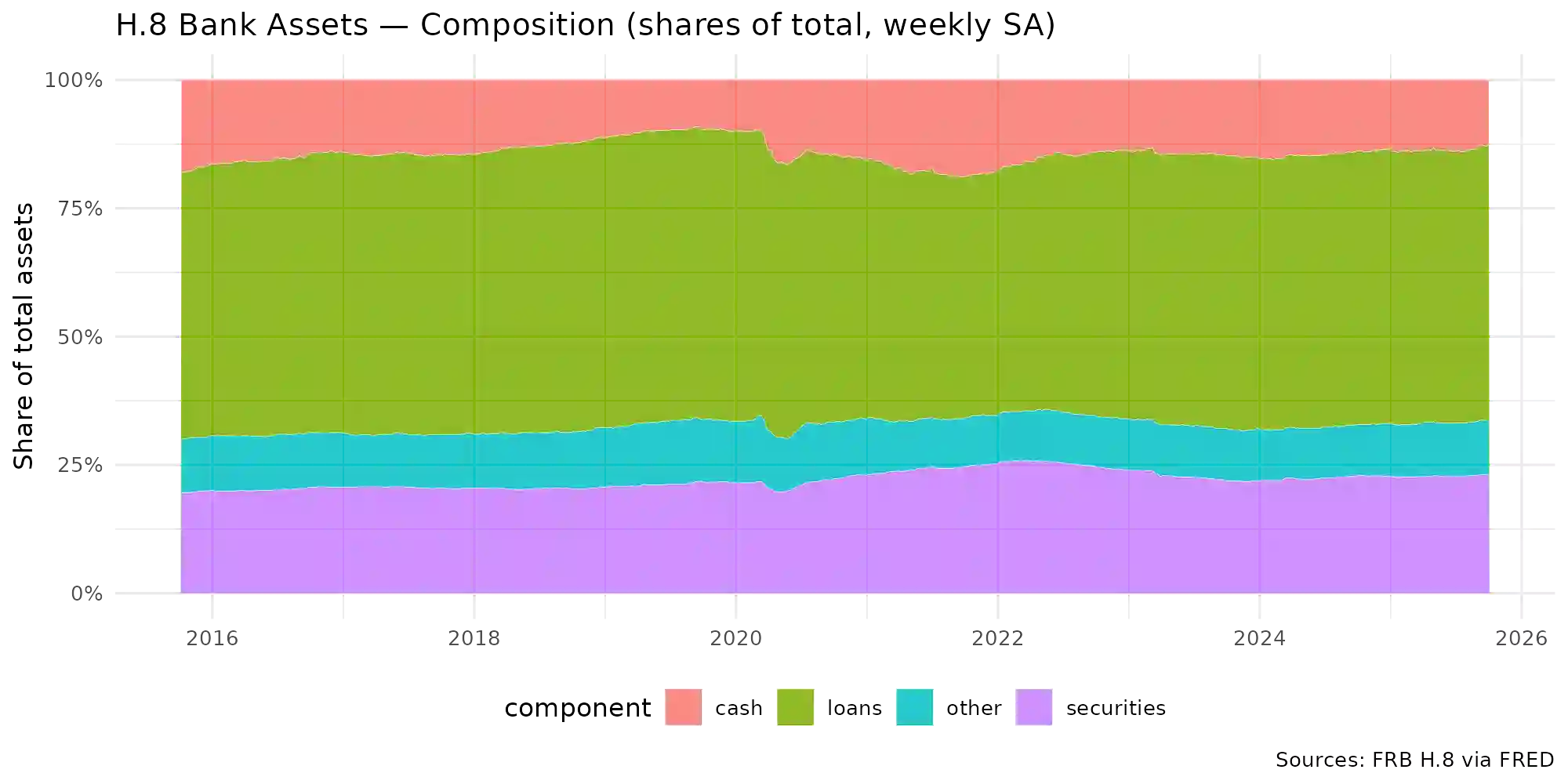
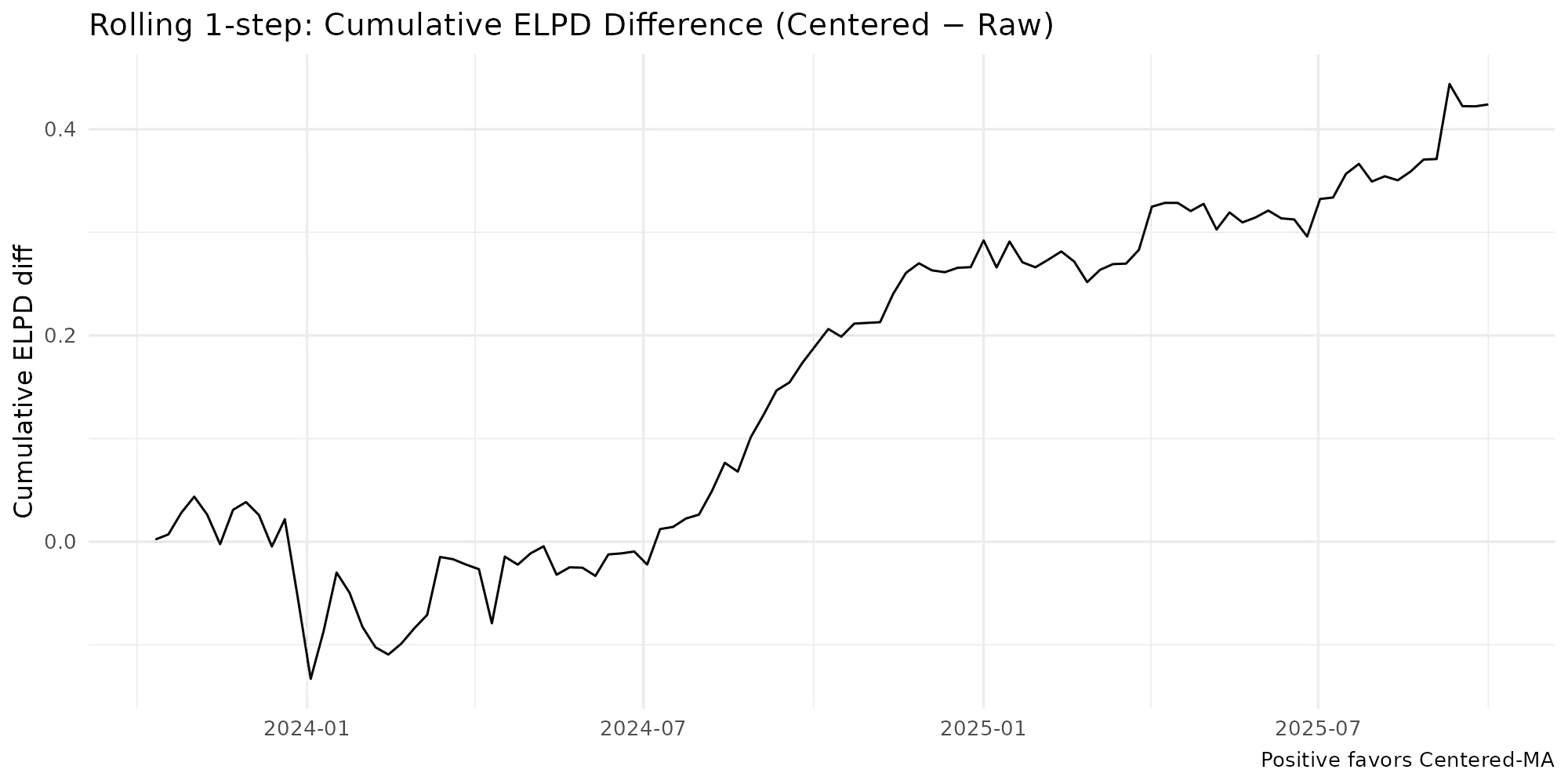
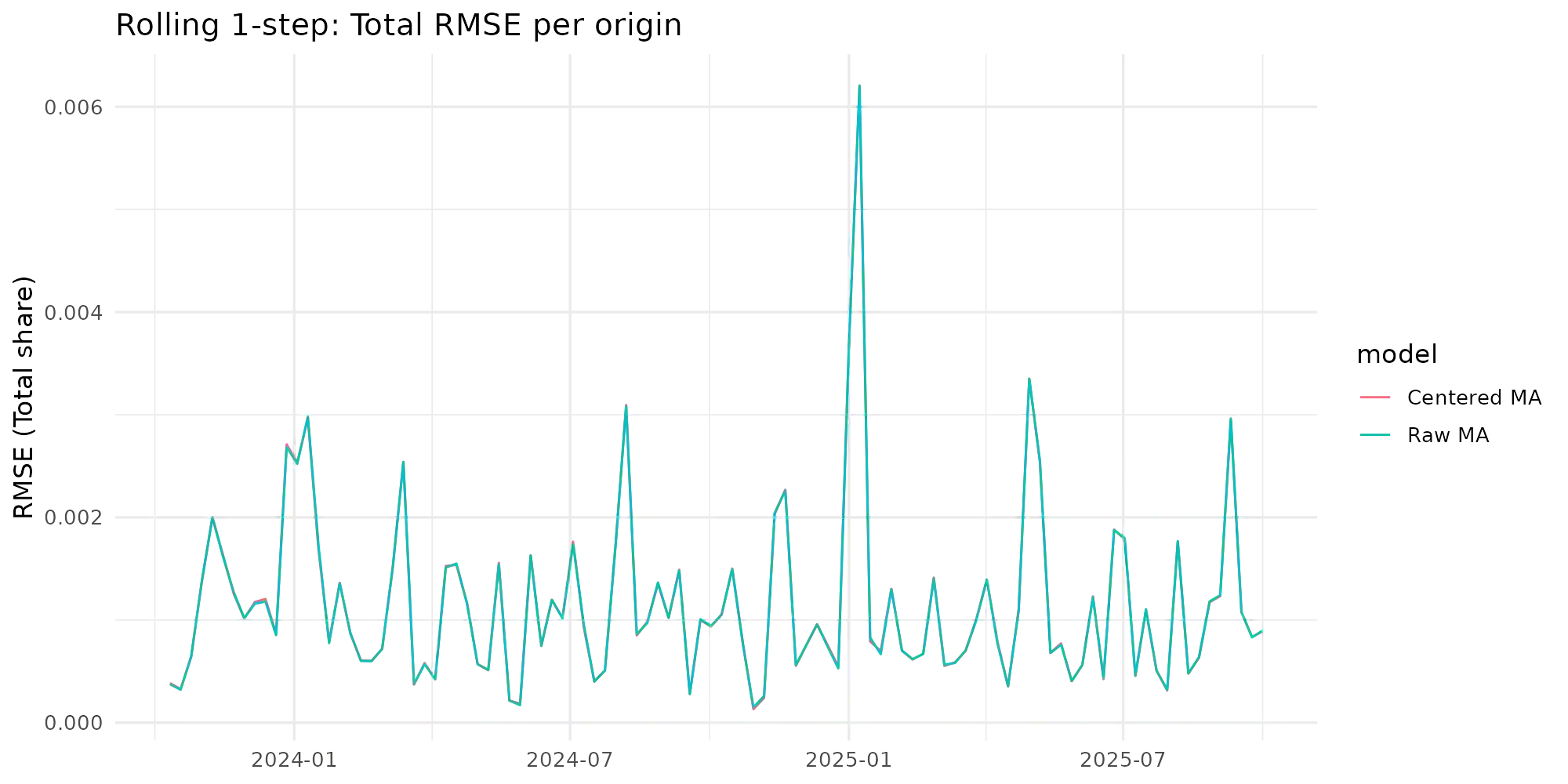
Observation-driven Dirichlet models for compositional time series commonly use the additive log-ratio (ALR) link and include a moving-average (MA) term based on ALR residuals. In the standard Bayesian Dirichlet Auto-Regressive Moving-Average (B-DARMA) recursion, this MA regressor has a nonzero conditional mean under the Dirichlet likelihood, which biases the mean path and complicates interpretation of the MA coefficients. We propose a minimal change: replace the raw regressor with a centered innovation equal to the ALR residual minus its conditional expectation, computable in closed form using digamma functions. Centering restores mean-zero innovations for the MA block without altering either the likelihood or the ALR link. We provide closed-form identities for the conditional mean and forecast recursion, show first-order equivalence to a digamma-link DARMA while retaining a simple inverse back to the mean composition, and supply ready-to-use code. In a weekly application to the Federal Reserve H.8 bank-asset composition, the centered specification improves log predictive scores with virtually identical point accuracy and markedly cleaner Hamiltonian Monte Carlo diagnostics.

翻译：针对成分时间序列的观测驱动Dirichlet模型通常采用加性对数比（ALR）连接函数，并包含基于ALR残差的移动平均（MA）项。在标准贝叶斯Dirichlet自回归移动平均（B-DARMA）递推中，该MA回归量在Dirichlet似然下具有非零条件均值，这会偏置均值路径并使得MA系数的解释复杂化。我们提出一个最小化改动方案：将原始回归量替换为中心化新息，即ALR残差减去其条件期望，该期望可通过digamma函数以闭合形式计算。中心化处理可在不改变似然函数或ALR连接函数的前提下，为MA模块恢复零均值新息。我们给出了条件均值与预测递推的闭合形式恒等式，证明其一阶等价于digamma连接DARMA模型，同时保持向均值成分的简单逆映射，并提供了可直接使用的代码。在美联储H.8银行资产成分的周度数据应用中，中心化设定显著提升了对数预测评分，其点预测精度几乎相同，且哈密顿蒙特卡洛诊断结果明显更清晰。