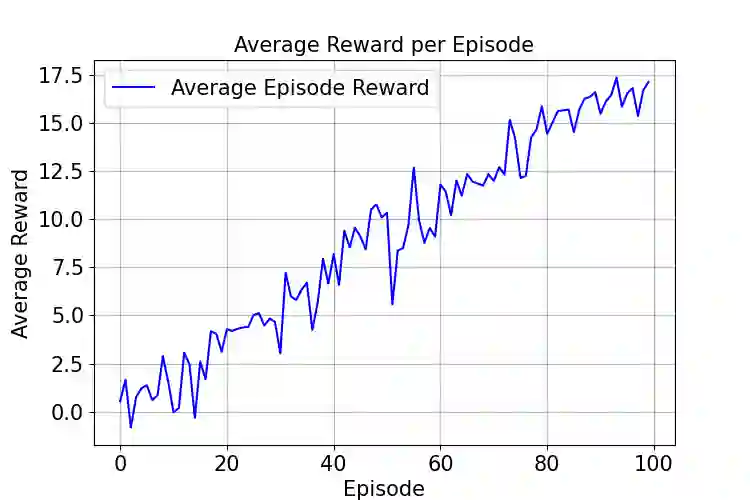
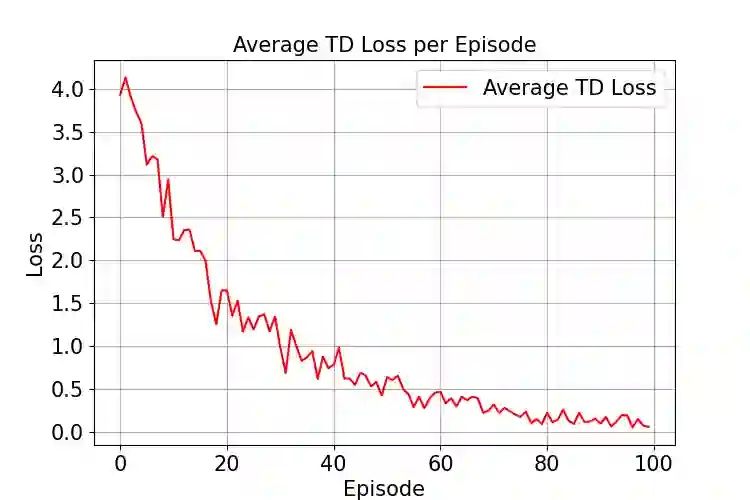
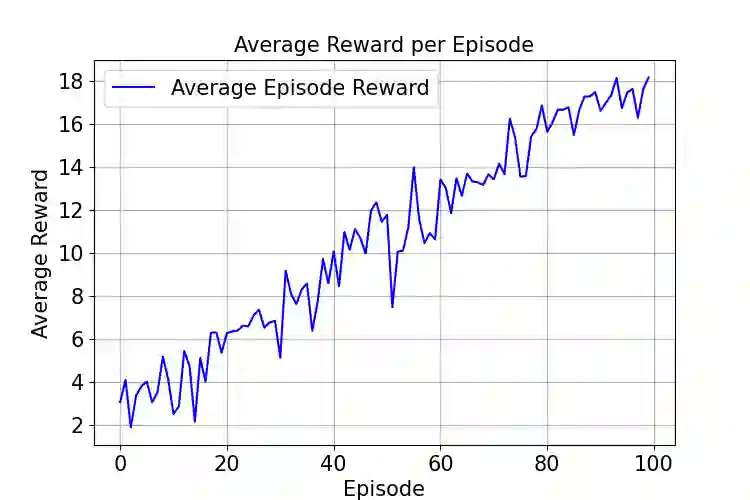
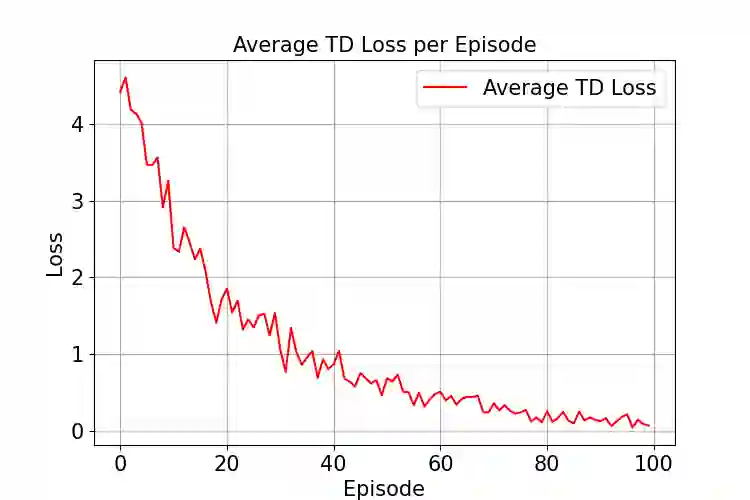
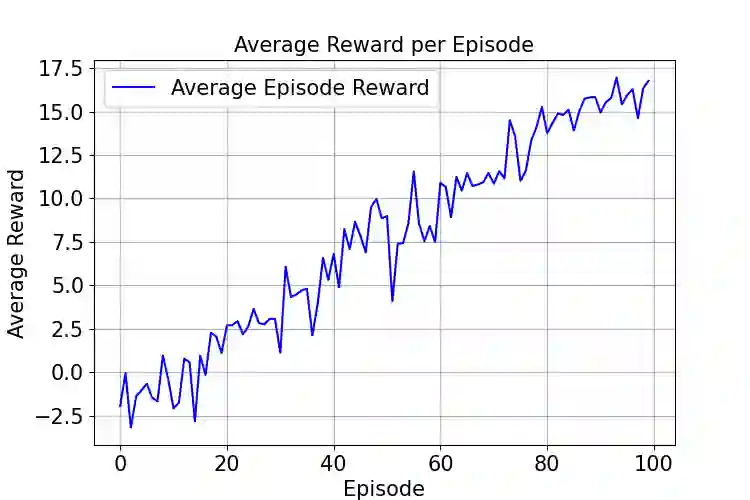
We propose a reinforcement learning (RL) framework for adaptive precision tuning of linear solvers, and can be extended to general algorithms. The framework is formulated as a contextual bandit problem and solved using incremental action-value estimation with a discretized state space to select optimal precision configurations for computational steps, balancing precision and computational efficiency. To verify its effectiveness, we apply the framework to iterative refinement for solving linear systems $Ax = b$. In this application, our approach dynamically chooses precisions based on calculated features from the system. In detail, a Q-table maps discretized features (e.g., approximate condition number and matrix norm)to actions (chosen precision configurations for specific steps), optimized via an epsilon-greedy strategy to maximize a multi-objective reward balancing accuracy and computational cost. Empirical results demonstrate effective precision selection, reducing computational cost while maintaining accuracy comparable to double-precision baselines. The framework generalizes to diverse out-of-sample data and offers insight into utilizing RL precision selection for other numerical algorithms, advancing mixed-precision numerical methods in scientific computing. To the best of our knowledge, this is the first work on precision autotuning with RL and verified on unseen datasets.

翻译：我们提出了一种用于线性求解器自适应精度调优的强化学习框架，该框架可扩展至通用算法。该框架被建模为上下文赌博机问题，并采用离散化状态空间的增量动作价值估计方法进行求解，以选择计算步骤的最优精度配置，从而平衡精度与计算效率。为验证其有效性，我们将该框架应用于求解线性方程组 $Ax = b$ 的迭代精化算法。在此应用中，我们的方法根据系统计算特征动态选择精度。具体而言，通过Q表将离散化特征（如近似条件数与矩阵范数）映射到动作（特定步骤选择的精度配置），并采用ε-贪婪策略进行优化，以最大化平衡精度与计算成本的多目标奖励函数。实验结果表明，该方法能实现有效的精度选择，在保持与双精度基准相当精度的同时显著降低计算成本。该框架可泛化至多样化的样本外数据，并为其他数值算法应用强化学习精度选择提供了思路，推动了科学计算中混合精度数值方法的发展。据我们所知，这是首个基于强化学习的精度自动调优研究，并在未见数据集上得到验证。