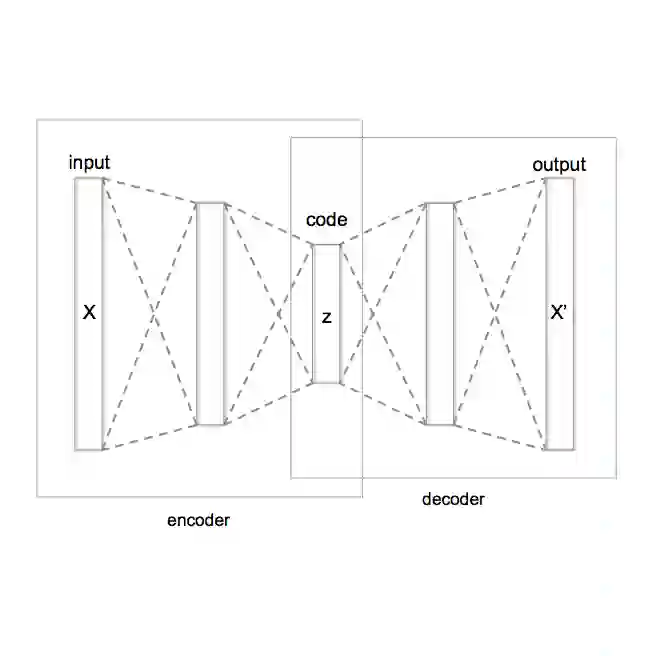
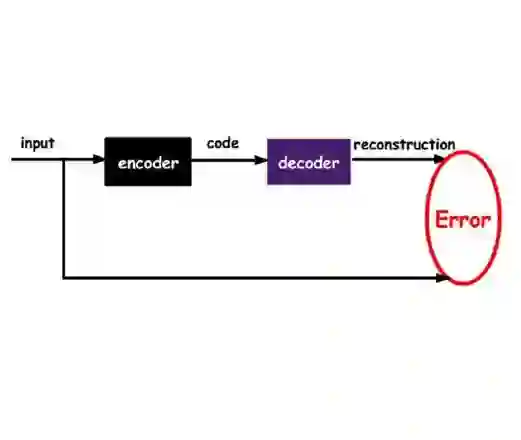
Variational Autoencoder is typically understood from the perspective of probabilistic inference. In this work, we propose a new geometric reinterpretation which complements the probabilistic view and enhances its intuitiveness. We demonstrate that the proper construction of semantic manifolds arises primarily from the constraining effect of the KL divergence on the encoder. We view the latent representations as a Gaussian ball rather than deterministic points. Under the constraint of KL divergence, Gaussian ball regularizes the latent space, promoting a more uniform distribution of encodings. Furthermore, we show that reparameterization establishes a critical contractual mechanism between the encoder and decoder, enabling the decoder to learn how to reconstruct from these stochastic regions. We further connect this viewpoint with VQ-VAE, offering a unified perspective: VQ-VAE can be seen as an autoencoder where encodings are constrained to a set of cluster centers, with its generative capability arising from the compactness rather than its stochasticity. This geometric framework provides a new lens for understanding how VAE shapes the latent geometry to enable effective generation.

翻译：变分自编码器通常从概率推断的角度被理解。本文提出一种新的几何重释，该视角补充了概率观点并增强了其直观性。我们证明，语义流形的恰当构建主要源于KL散度对编码器的约束作用。我们将潜在表示视为高斯球而非确定性点。在KL散度的约束下，高斯球对潜在空间进行正则化，促使编码分布更加均匀。此外，我们证明重参数化在编码器与解码器之间建立了关键的契约机制，使解码器能够学习如何从这些随机区域进行重构。我们进一步将此观点与VQ-VAE相联系，提供一个统一视角：VQ-VAE可被视为编码被约束至一组聚类中心的自编码器，其生成能力源于紧致性而非随机性。这一几何框架为理解VAE如何塑造潜在几何以实现有效生成提供了新的视角。