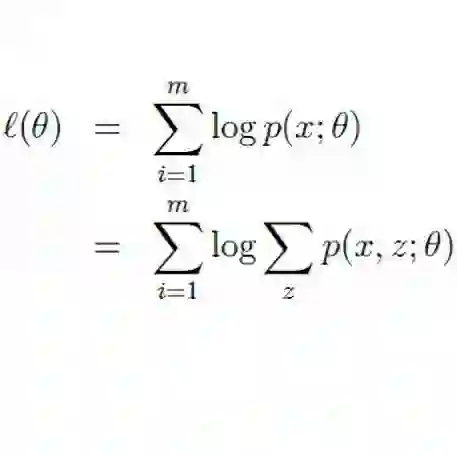We study the expectation-maximization (EM) algorithm for general latent-variable models under (i) distributional misspecification and (ii) nonidentifiability induced by a group action. We formulate EM on the quotient parameter space and measure error using an arbitrary integral probability metric (IPM). Our main results give (a) a sharp local linear convergence rate for population EM governed by the spectral radius of the linearization on a local slice, and (b) tight finite-sample bounds for sample EM obtained via perturbed contraction inequalities and generic chaining/entropy control of EM-induced empirical processes.

翻译：本研究探讨期望最大化（EM）算法在（i）分布误设与（ii）群作用导致的不可识别性条件下，在一般隐变量模型中的应用。我们在商参数空间上构建EM算法框架，并采用任意积分概率度量（IPM）衡量误差。主要研究成果包括：（a）通过局部切片线性化谱半径刻画总体EM的尖锐局部线性收敛率；（b）结合扰动收缩不等式与EM诱导经验过程的通用链式/熵控制方法，获得样本EM的紧致有限样本界。