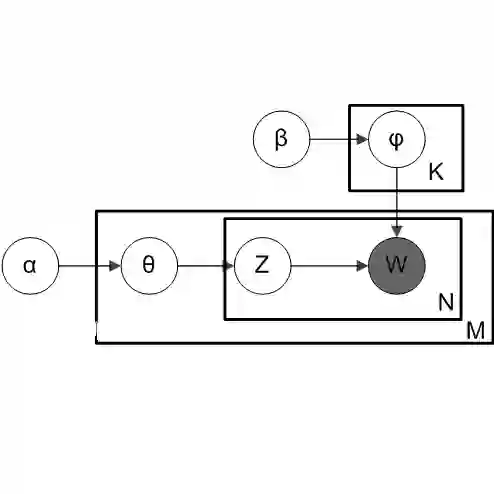
We revisit Deep Linear Discriminant Analysis (Deep LDA) from a likelihood-based perspective. While classical LDA is a simple Gaussian model with linear decision boundaries, attaching an LDA head to a neural encoder raises the question of how to train the resulting deep classifier by maximum likelihood estimation (MLE). We first show that end-to-end MLE training of an unconstrained Deep LDA model ignores discrimination: when both the LDA parameters and the encoder parameters are learned jointly, the likelihood admits a degenerate solution in which some of the class clusters may heavily overlap or even collapse, and classification performance deteriorates. Batchwise moment re-estimation of the LDA parameters does not remove this failure mode. We then propose a constrained Deep LDA formulation that fixes the class means to the vertices of a regular simplex in the latent space and restricts the shared covariance to be spherical, leaving only the priors and a single variance parameter to be learned along with the encoder. Under these geometric constraints, MLE becomes stable and yields well-separated class clusters in the latent space. On images (Fashion-MNIST, CIFAR-10, CIFAR-100), the resulting Deep LDA models achieve accuracy competitive with softmax baselines while offering a simple, interpretable latent geometry that is clearly visible in two-dimensional projections.

翻译：我们从基于似然的角度重新审视深度线性判别分析（Deep LDA）。经典的LDA是一个具有线性决策边界的简单高斯模型，而将LDA头连接到神经编码器上，则引出了如何通过最大似然估计（MLE）来训练由此产生的深度分类器的问题。我们首先证明，对无约束的Deep LDA模型进行端到端的MLE训练会忽略判别性：当LDA参数和编码器参数被联合学习时，似然函数存在一个退化解，其中某些类别的聚类可能严重重叠甚至坍缩，导致分类性能下降。对LDA参数进行逐批次矩重估计并不能消除这种失效模式。接着，我们提出了一种带约束的Deep LDA公式，它将潜在空间中的类别均值固定在一个规则单纯形的顶点上，并将共享协方差限制为球形，仅留下先验概率和一个方差参数与编码器一起学习。在这些几何约束下，MLE变得稳定，并在潜在空间中产生良好分离的类别聚类。在图像数据集（Fashion-MNIST, CIFAR-10, CIFAR-100）上，由此得到的Deep LDA模型实现了与softmax基线相竞争的准确率，同时提供了一个简单、可解释的潜在几何结构，该结构在二维投影中可以清晰地观察到。