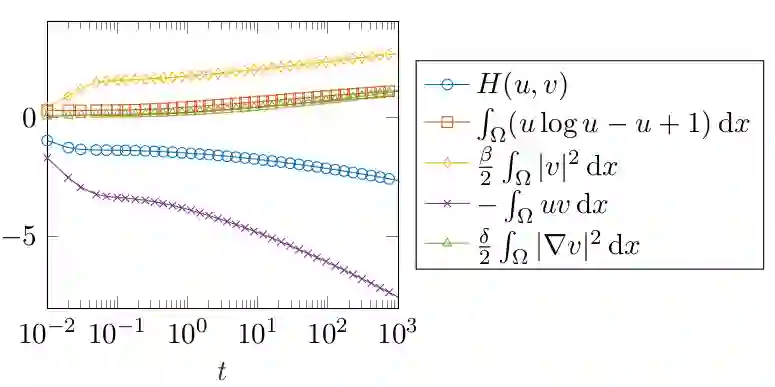
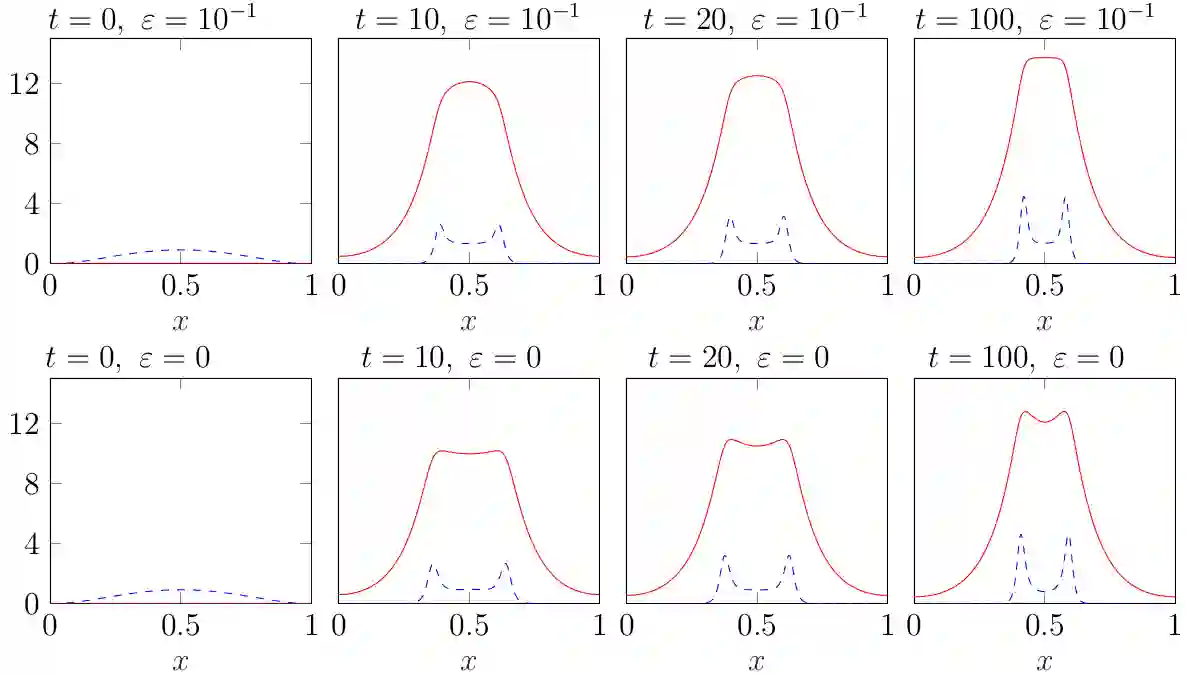
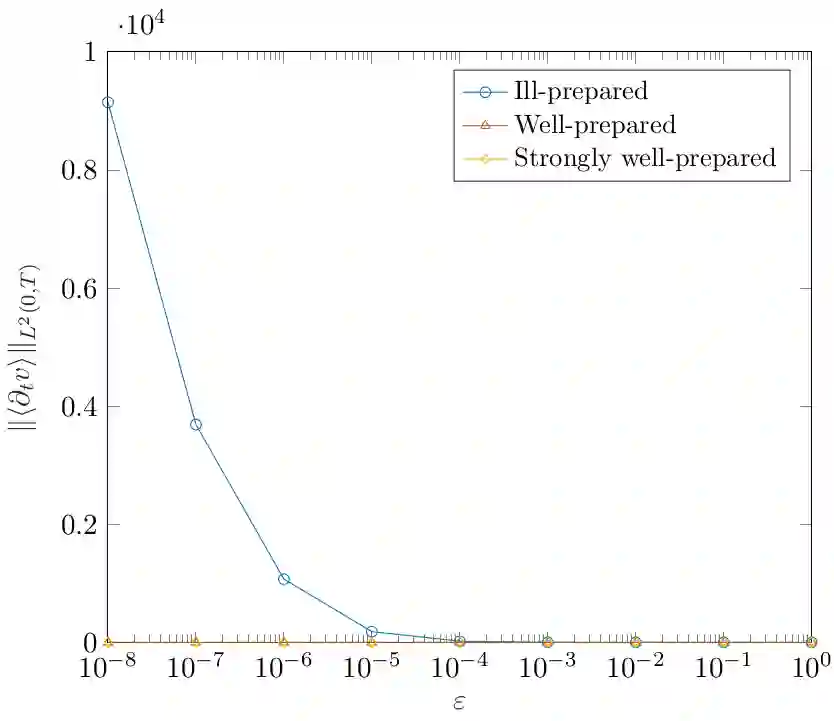
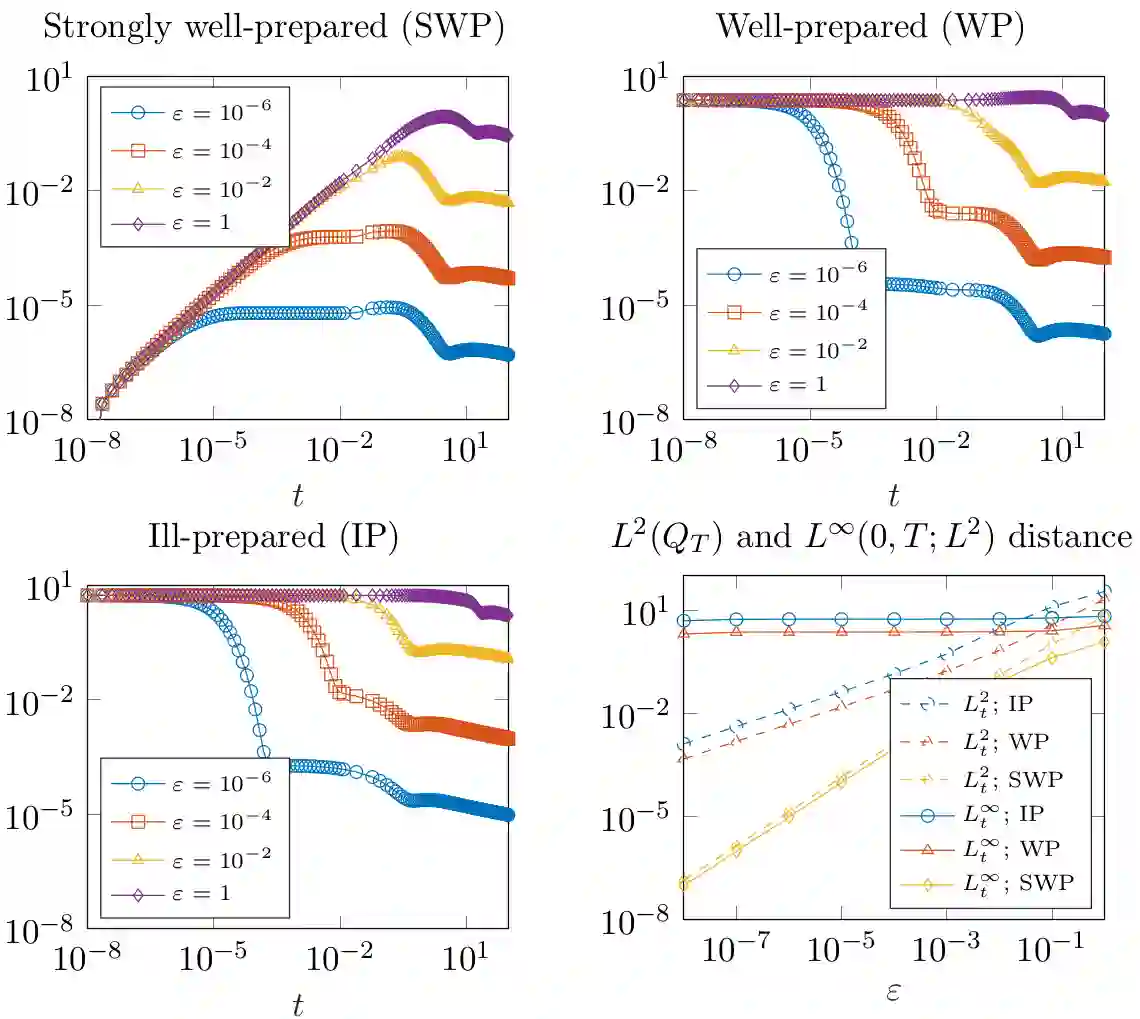
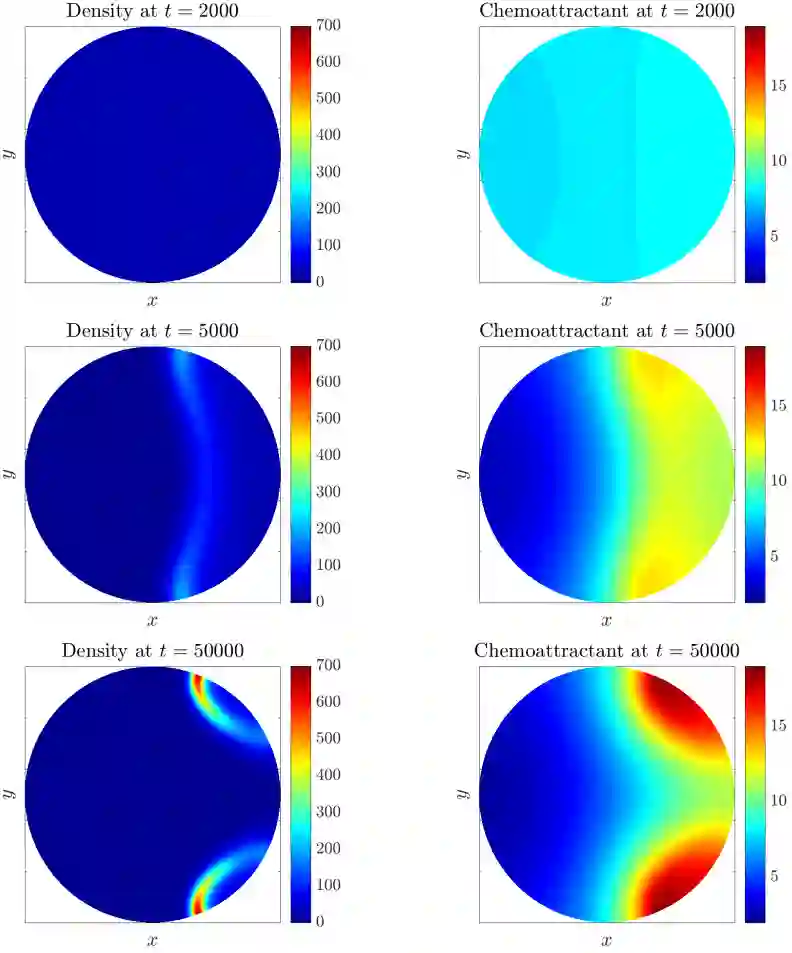
In this paper we design, analyze and simulate a finite volume scheme for a cross-diffusion system which models chemotaxis with local sensing. This system has the same Lyapunov function (or entropy) as the celebrated minimal Keller-Segel system, but unlike the latter, its solutions are known to exist globally in 2D. The long-time behavior of solutions is only partially understood which motivates numerical exploration with a reliable numerical method. We propose a linearly implicit, two-point flux finite volume approximation of the system. We show that the scheme preserves, at the discrete level, the main features of the continuous system, namely mass conservation, non-negativity of solution, entropy dissipation, and duality estimates. These properties allow us to prove the well-posedness, unconditional stability and convergence of the scheme. We also show rigorously that the scheme possesses an asymptotic preserving (AP) property in the quasi-stationary limit. We complement our analysis with thorough numerical experiments investigating convergence and AP properties of the scheme as well as its reliability with respect to stability properties of steady solutions.

翻译：本文针对局部感知趋化交叉扩散系统设计、分析并模拟了一种有限体积格式。该系统与著名的极小Keller-Segel模型具有相同的李雅普诺夫函数（或称熵），但不同于后者，该系统的解在二维情况下被证明具有全局存在性。目前对解长时间行为的理解尚不完整，这促使我们采用可靠的数值方法进行探索。我们提出了一种线性隐式、两点通量的有限体积近似格式。我们证明该格式在离散层面保持了连续系统的主要特征：质量守恒、解的非负性、熵耗散特性以及对偶估计。这些性质使我们能够证明格式的适定性、无条件稳定性和收敛性。我们严格证明了该格式在准静态极限下具有渐近保持（AP）特性。通过详尽的数值实验，我们进一步验证了格式的收敛性与AP特性，并检验了其关于稳态解稳定性分析的可靠性。