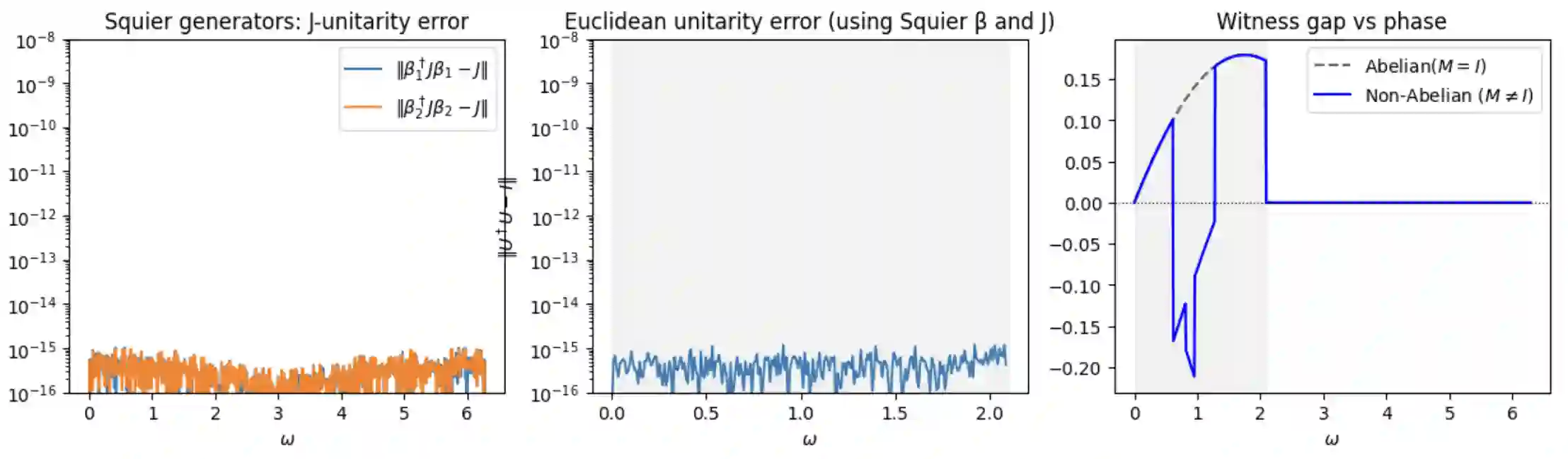
We introduce a frequency-tunable, two-dimensional non-Abelian control of operation order constructed from the reduced Burau representation of the braid group $B_3$, specialised at $t=e^{i\omega}$ and unitarized by Squier's Hermitian form. Coupled to two non-commuting qubit unitaries $A,B$, the resulting switch admits a closed expression for the single-shot Helstrom success probability and a fixed-order ceiling $p_{\mathrm{fixed}}$, defining the analytic witness gap $\Delta(\omega)=p_{\mathrm{switch}}(\omega)-p_{\mathrm{fixed}}$. The sign change of $\Delta(\omega)$ across the Squier positivity window reveals alternating constructive and destructive interference of causal orders, a hallmark of non-Abelian control, while $\Delta(\omega)>0$ certifies algebraic causal non-separability. Numerical simulations confirm both enhancement and suppression regimes, establishing a minimal $B_3$ braid control that reproduces the characteristic interference pattern expected from a Gedankenexperiment in anyonic statistics.

翻译：本文引入一种频率可调、二维的非阿贝尔操作顺序控制方案，该方案基于辫群$B_3$的约化Burau表示（在$t=e^{i\omega}$处取值）并通过Squier埃尔米特形式进行酉化。当与两个非对易的量子比特酉算子$A,B$耦合时，所得开关算符可给出单次Helstrom成功概率的闭式表达式，并存在一个固定顺序上限$p_{\mathrm{fixed}}$，由此定义解析见证间隙$\Delta(\omega)=p_{\mathrm{switch}}(\omega)-p_{\mathrm{fixed}}$。$\Delta(\omega)$在Squier正性窗口内随频率改变符号，揭示了因果顺序交替出现的相长与相消干涉，这是非阿贝尔控制的典型特征；而$\Delta(\omega)>0$则认证了代数因果不可分离性。数值模拟同时确认了增强与抑制两种区域，从而建立了一个最小化的$B_3$辫群控制模型，该模型重现了任意子统计思想实验中预期的特征干涉图样。