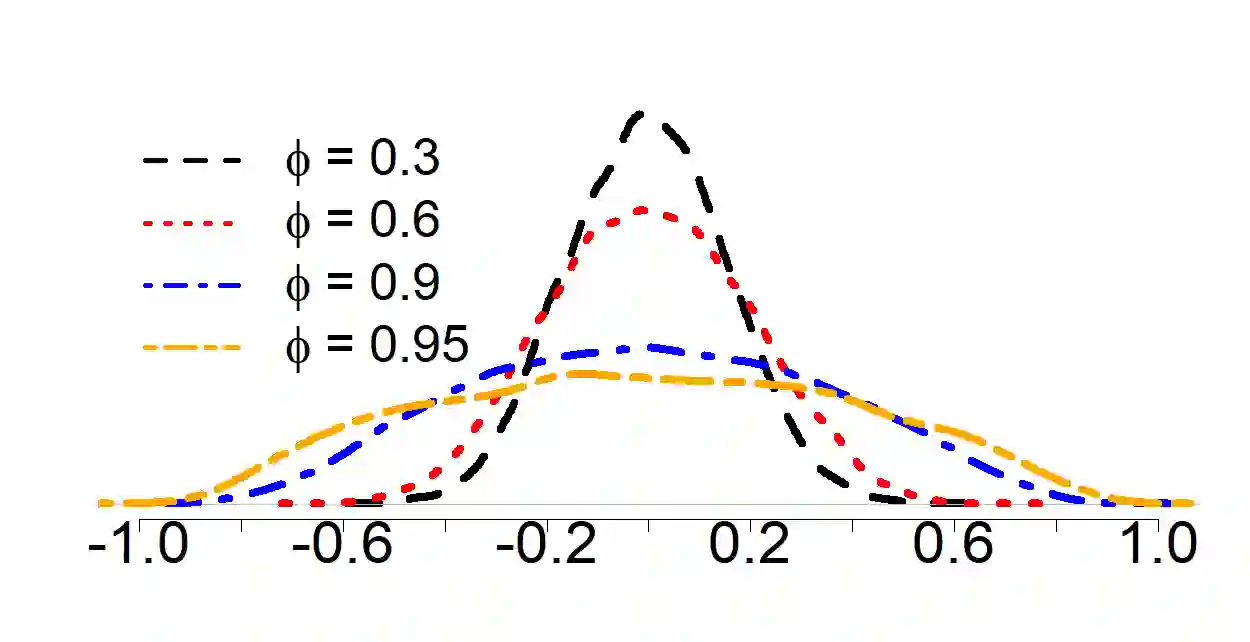
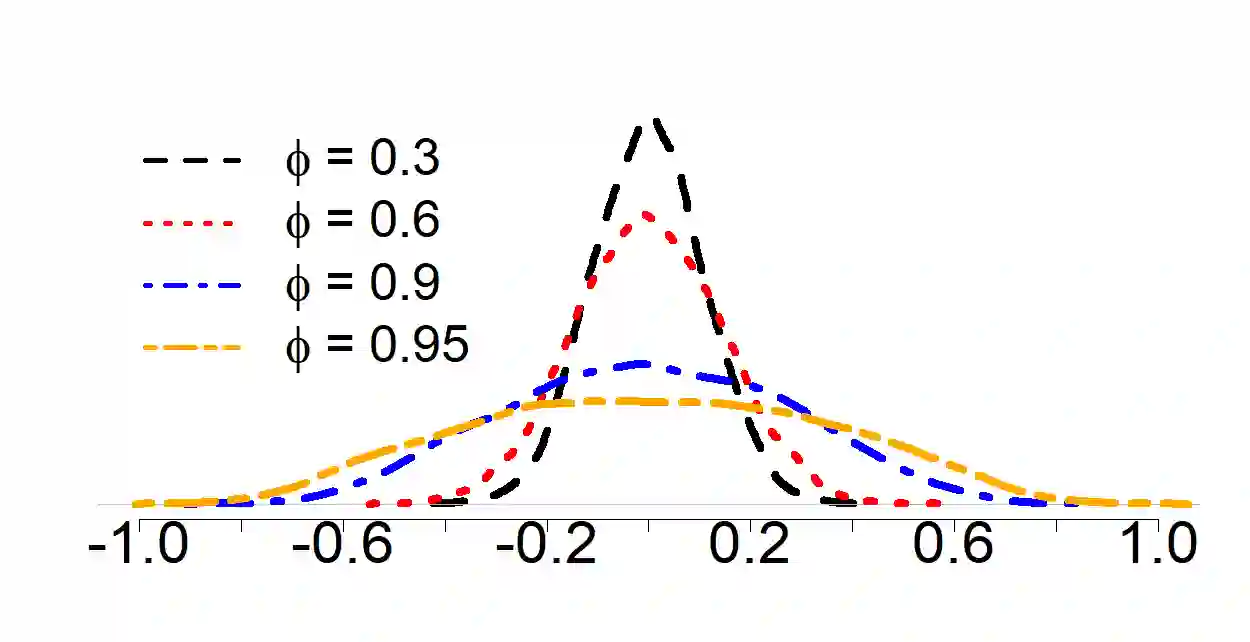
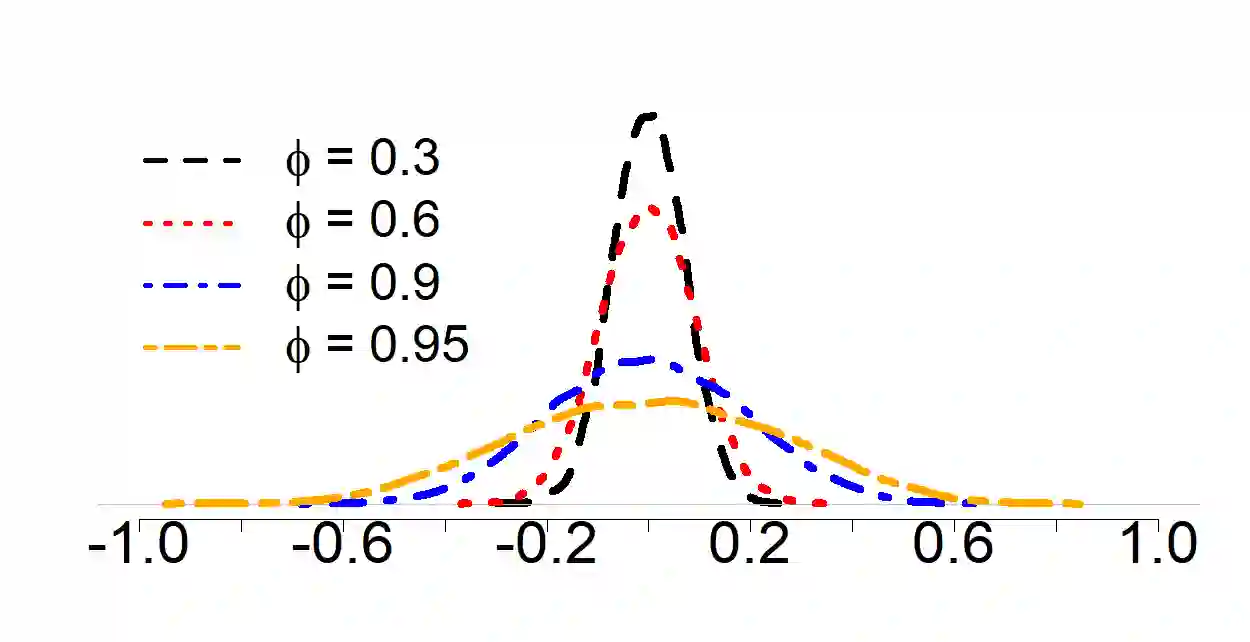
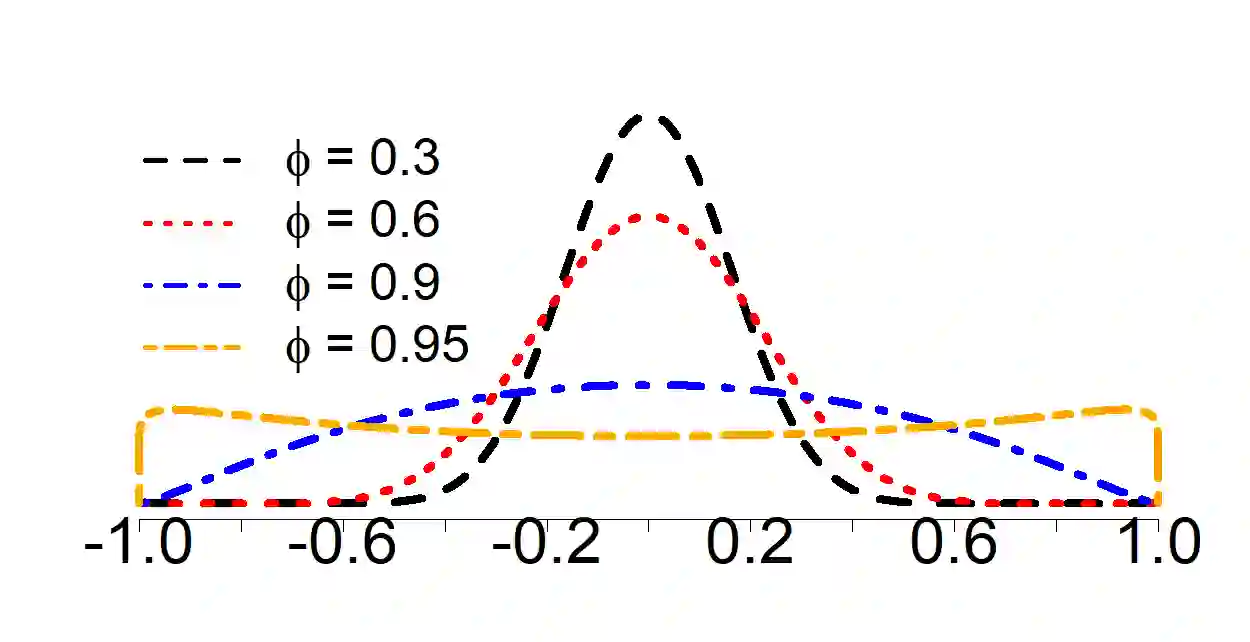
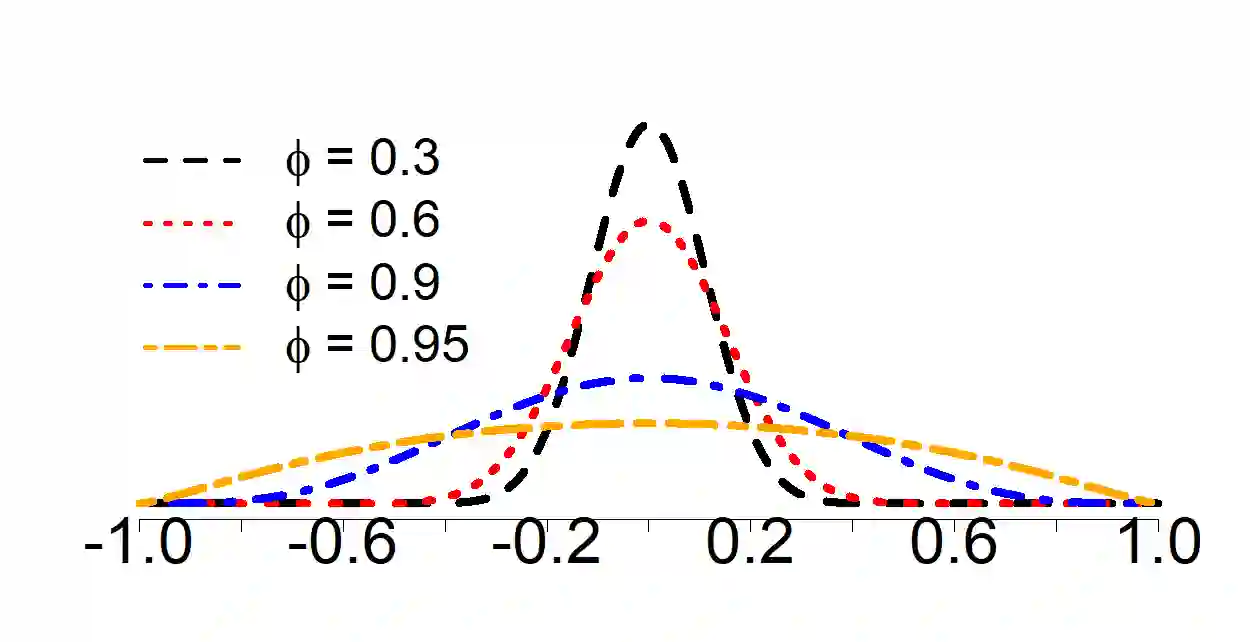
We explore estimation and forecast accuracy for sparse linear models, focusing on scenarios where both predictors and errors carry serial correlations. We establish a clear link between predictor serial correlation and the performance of the LASSO, showing that even orthogonal or weakly correlated stationary AR processes can lead to significant spurious correlations due to their serial correlations. To address this challenge, we propose a novel approach named ARMAr-LASSO ({\em ARMA residuals LASSO}), which applies the LASSO to predictors that have been pre-whitened with ARMA filters and lags of dependent variable. We derive both asymptotic results and oracle inequalities for the ARMAr-LASSO, demonstrating that it effectively reduces estimation errors while also providing an effective forecasting and feature selection strategy. Our findings are supported by extensive simulations and an application to real-world macroeconomic data, which highlight the superior performance of the ARMAr-LASSO for handling sparse linear models in the context of time series.

翻译：本文探讨了稀疏线性模型的估计与预测精度，重点关注预测变量与误差项均存在序列相关性的情形。我们建立了预测变量序列相关性与LASSO性能之间的明确联系，表明即使是正交或弱相关的平稳AR过程，由于其序列相关性，也可能导致显著的伪相关性。为应对这一挑战，我们提出了一种名为ARMAr-LASSO（ARMA残差LASSO）的新方法，该方法将LASSO应用于经过ARMA滤波器和因变量滞后项预白化处理的预测变量。我们推导了ARMAr-LASSO的渐近结果与Oracle不等式，证明其能有效降低估计误差，同时提供有效的预测与特征选择策略。大量仿真实验及对实际宏观经济数据的应用验证了我们的结论，突显了ARMAr-LASSO在处理时间序列背景下稀疏线性模型时的优越性能。