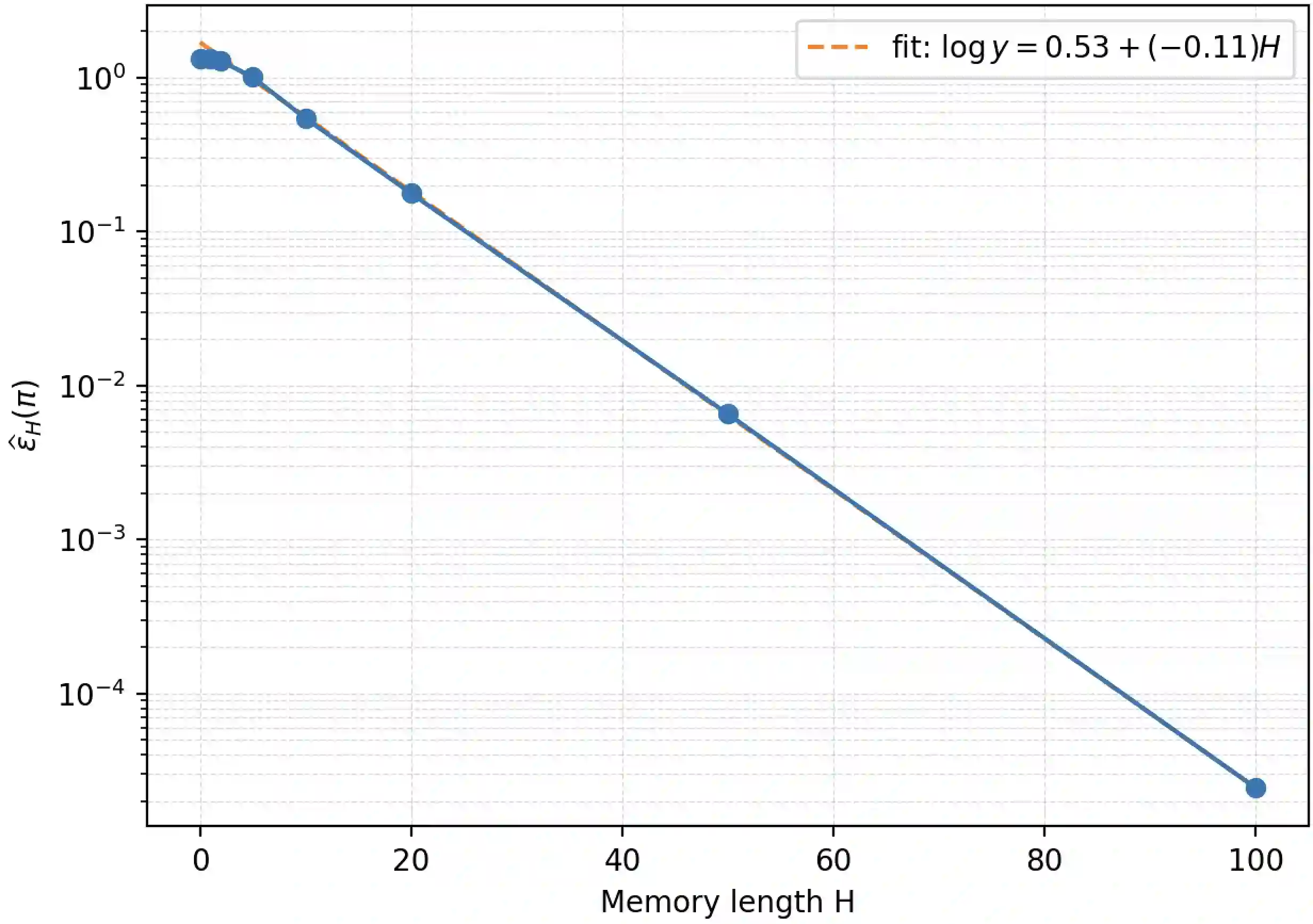
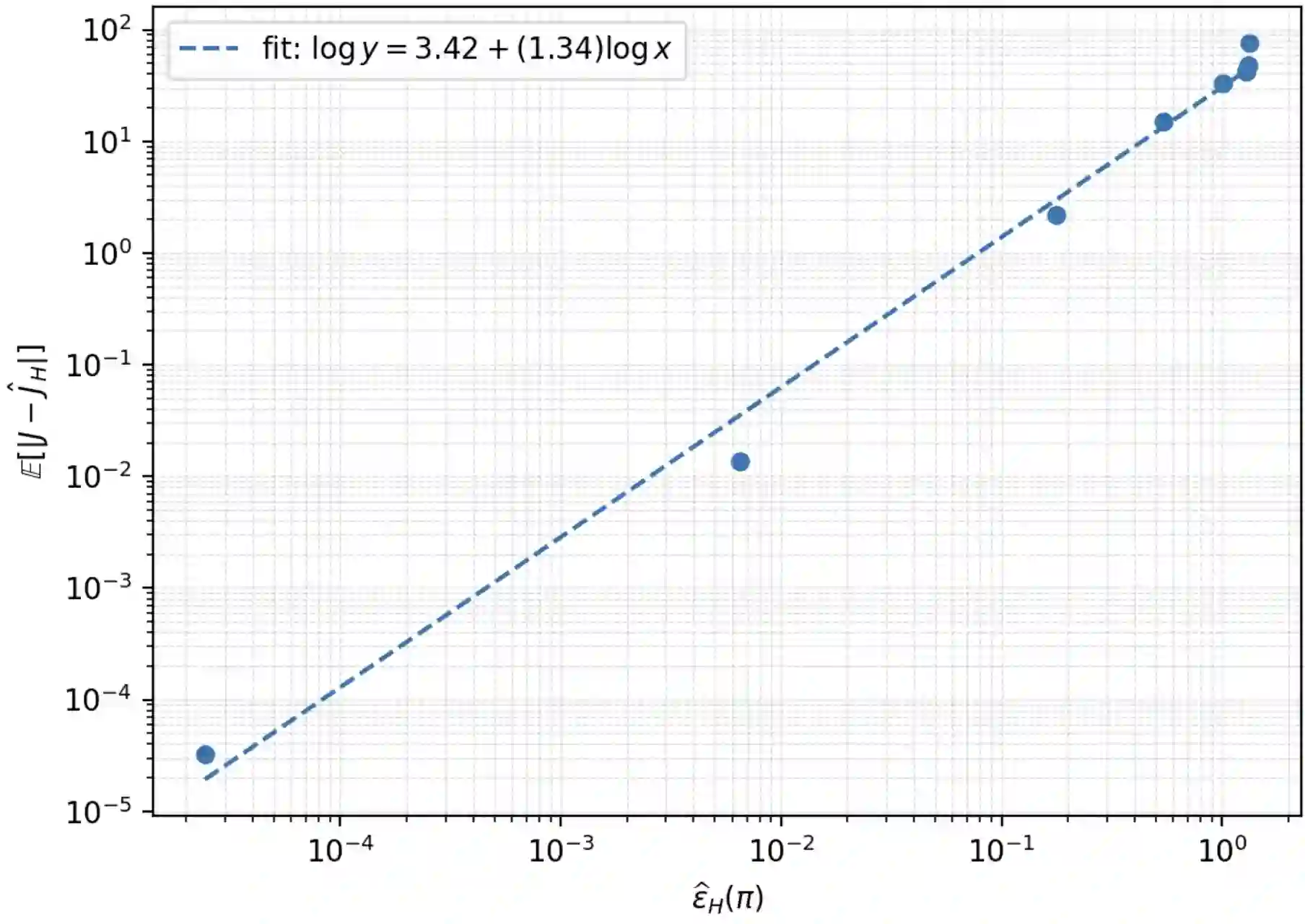
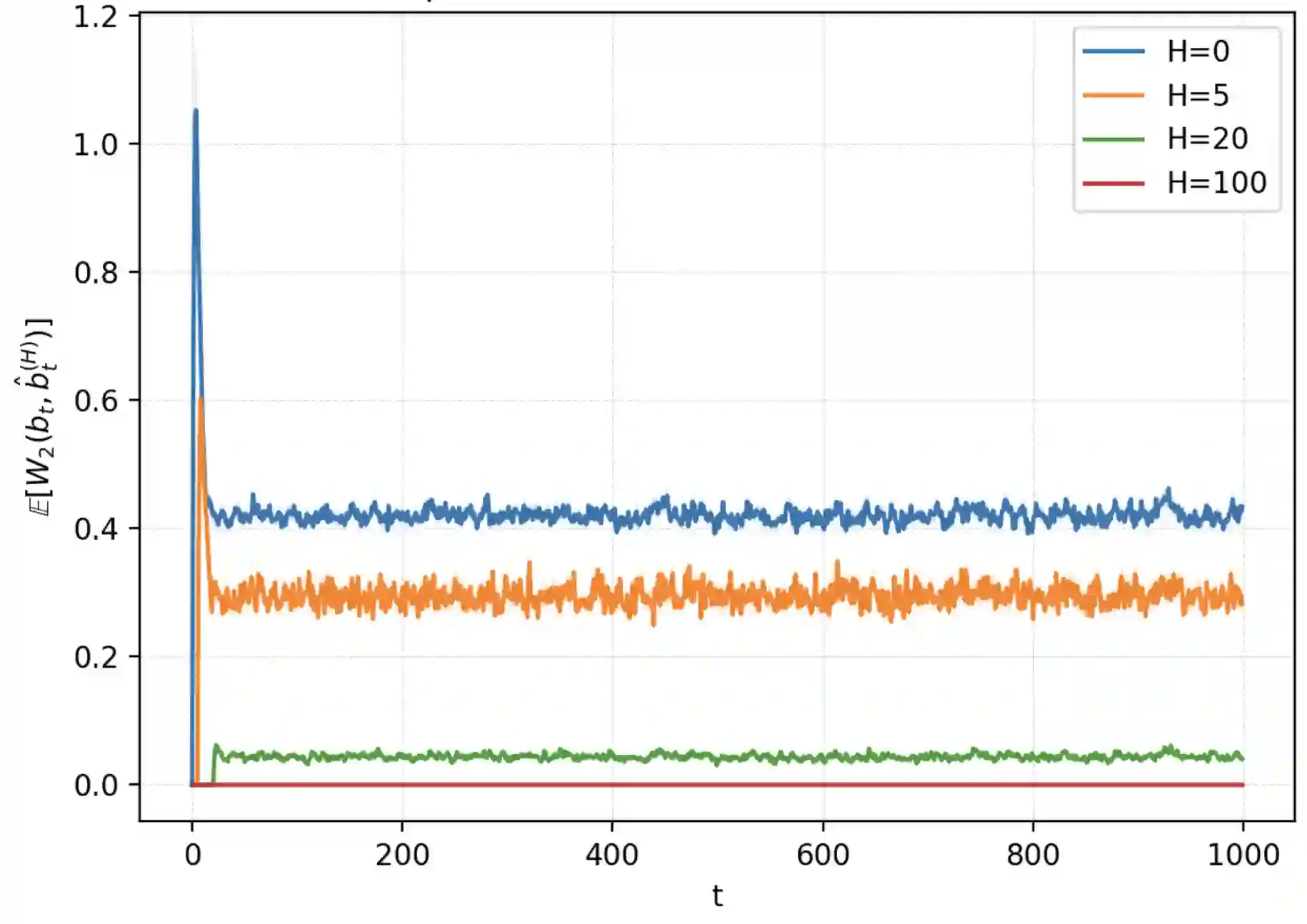
We study finite memory belief approximation for partially observable (PO) stochastic optimal control (SOC) problems. While belief states are sufficient for SOC in partially observable Markov decision processes (POMDPs), they are generally infinite-dimensional and impractical. We interpret truncated input-output (IO) histories as inducing a belief approximation and develop a metric-based theory that directly relates information loss to control performance. Using the Wasserstein metric, we derive policy-conditional performance bounds that quantify value degradation induced by finite memory along typical closed-loop trajectories. Our analysis proceeds via a fixed-policy comparison: we evaluate two cost functionals under the same closed-loop execution and isolate the effect of replacing the true belief by its finite memory approximation inside the belief-level cost. For linear quadratic Gaussian (LQG) systems, we provide closed-form belief mismatch evaluation and empirically validate the predicted mechanism, demonstrating that belief mismatch decays approximately exponentially with memory length and that the induced performance mismatch scales accordingly. Together, these results provide a metric-aware characterization of what finite memory belief approximation can and cannot achieve in PO settings.

翻译：本文研究部分可观测（PO）随机最优控制（SOC）问题中的有限记忆信念逼近方法。尽管信念状态对于部分可观测马尔可夫决策过程（POMDP）中的SOC问题具有充分性，但其通常为无限维且不具实用性。我们将截断的输入-输出（IO）历史序列解释为诱导信念逼近的手段，并建立了一套基于度量的理论，直接将信息损失与控制性能相关联。利用Wasserstein度量，我们推导出策略条件性能边界，该边界量化了典型闭环轨迹上由有限记忆引起的价值衰减。我们的分析通过固定策略比较展开：在同一闭环执行过程中评估两个成本泛函，并分离在信念层级成本函数中用有限记忆逼近替代真实信念所产生的影响。对于线性二次高斯（LQG）系统，我们给出了闭式信念失配评估方法，并通过实验验证了预测机制，证明信念失配随记忆长度近似指数衰减，且引发的性能失配相应缩放。这些结果共同提供了有限记忆信念逼近在PO场景中能力与局限的度量感知表征。