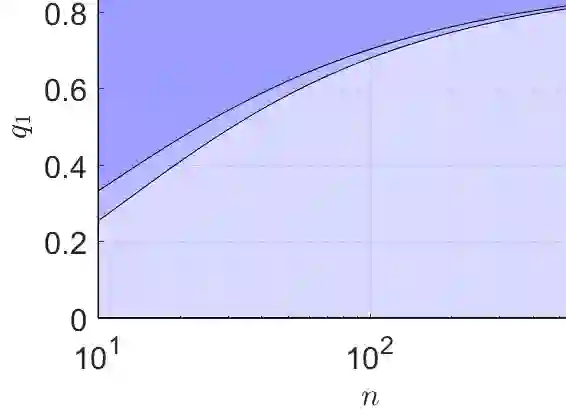
We consider the problem of learning from training data obtained in different contexts, where the test data is subject to distributional shifts. We develop a distributionally robust method that focuses on excess risks and achieves a more appropriate trade-off between performance and robustness than the conventional and overly conservative minimax approach. The proposed method is computationally feasible and provides statistical guarantees. We demonstrate its performance using both real and synthetic data.

翻译：我们考虑了从不同情况下获得的培训数据中学习的问题,在这些情况下,测试数据会发生分布变化;我们开发了一种分配上稳健的方法,侧重于超额风险,并在业绩和稳健性之间实现比传统和过于保守的小型最大方法更适当的权衡。提议的方法在计算上是可行的,并提供统计保证。我们用真实和合成数据来证明其绩效。