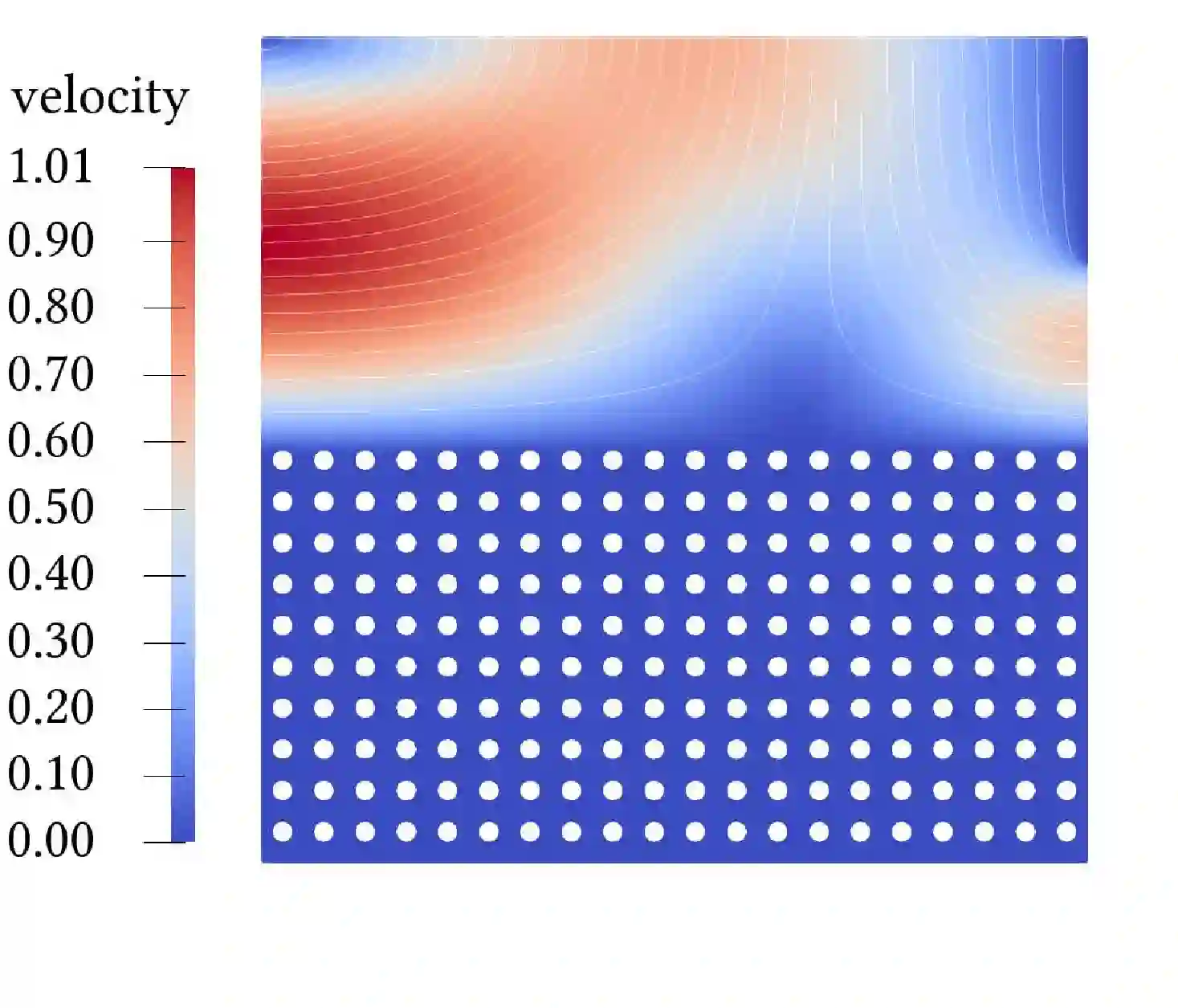
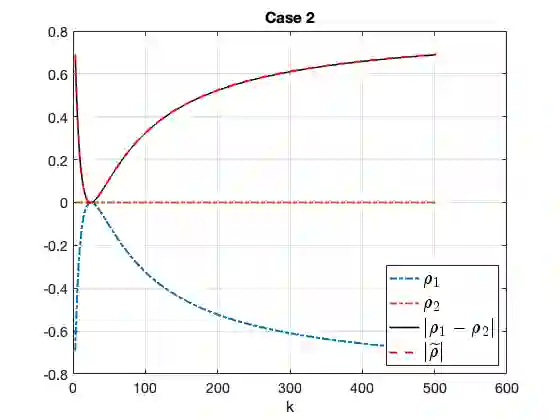
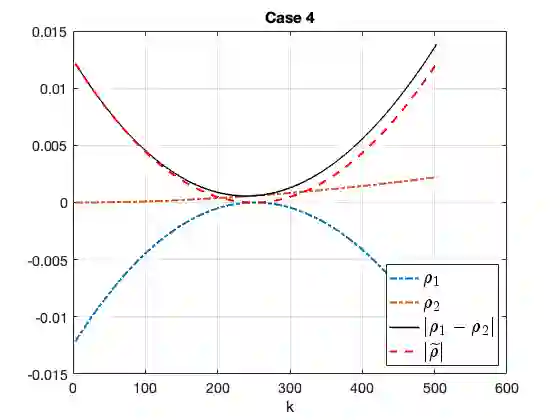
Due to their wide appearance in environmental settings as well as industrial and medical applications, the Stokes-Darcy problems with different sets of interface conditions establish an active research area in the community of mathematical modelers and computational scientists. For numerical simulation of such coupled problems in applications, robust and efficient computational algorithms are needed. In this work, we consider a generalization of the Beavers-Joseph interface condition recently developed using homogenization and boundary layer theory. This extension is applicable not only for the parallel flows to the fluid-porous interface as its predecessor, but also for arbitrary flow directions. To solve the Stokes-Darcy problem with these generalized interface conditions efficiently, we develop and analyze a Robin-Robin domain decomposition method using Fourier analysis to identify optimal weights in the Robin interface conditions. We study efficiency and robustness of the proposed method and provide numerical simulations which confirm the obtained theoretical results.

翻译：由于在不同环境场景及工业与医学应用中的广泛出现，采用各类界面条件的Stokes-Darcy问题已成为数学建模与计算科学领域活跃的研究方向。针对实际应用中此类耦合问题的数值模拟，需要开发鲁棒且高效的计算算法。本文基于均质化理论与边界层理论，对近期发展的Beavers-Joseph界面条件进行推广。该扩展不仅适用于平行于流体-多孔介质界面的流动（如其前身条件），还能处理任意方向的流动。为高效求解具有此类广义界面条件的Stokes-Darcy问题，我们通过傅里叶分析开发并分析了一种Robin-Robin区域分解方法，以确定Robin界面条件中的最优权重系数。我们研究了所提方法的效率与鲁棒性，并通过数值模拟验证了所得理论结果。