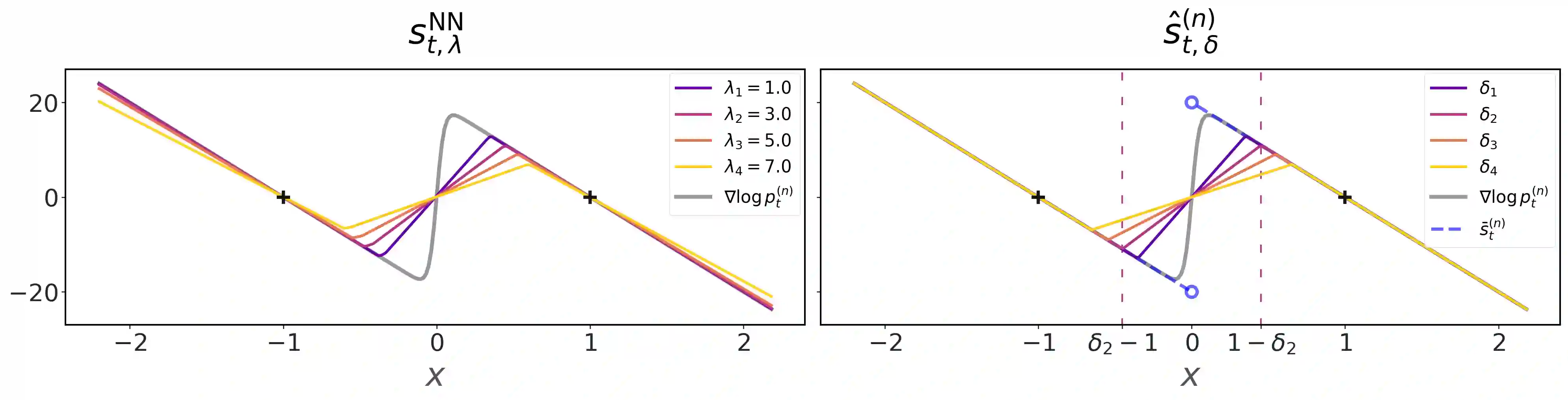
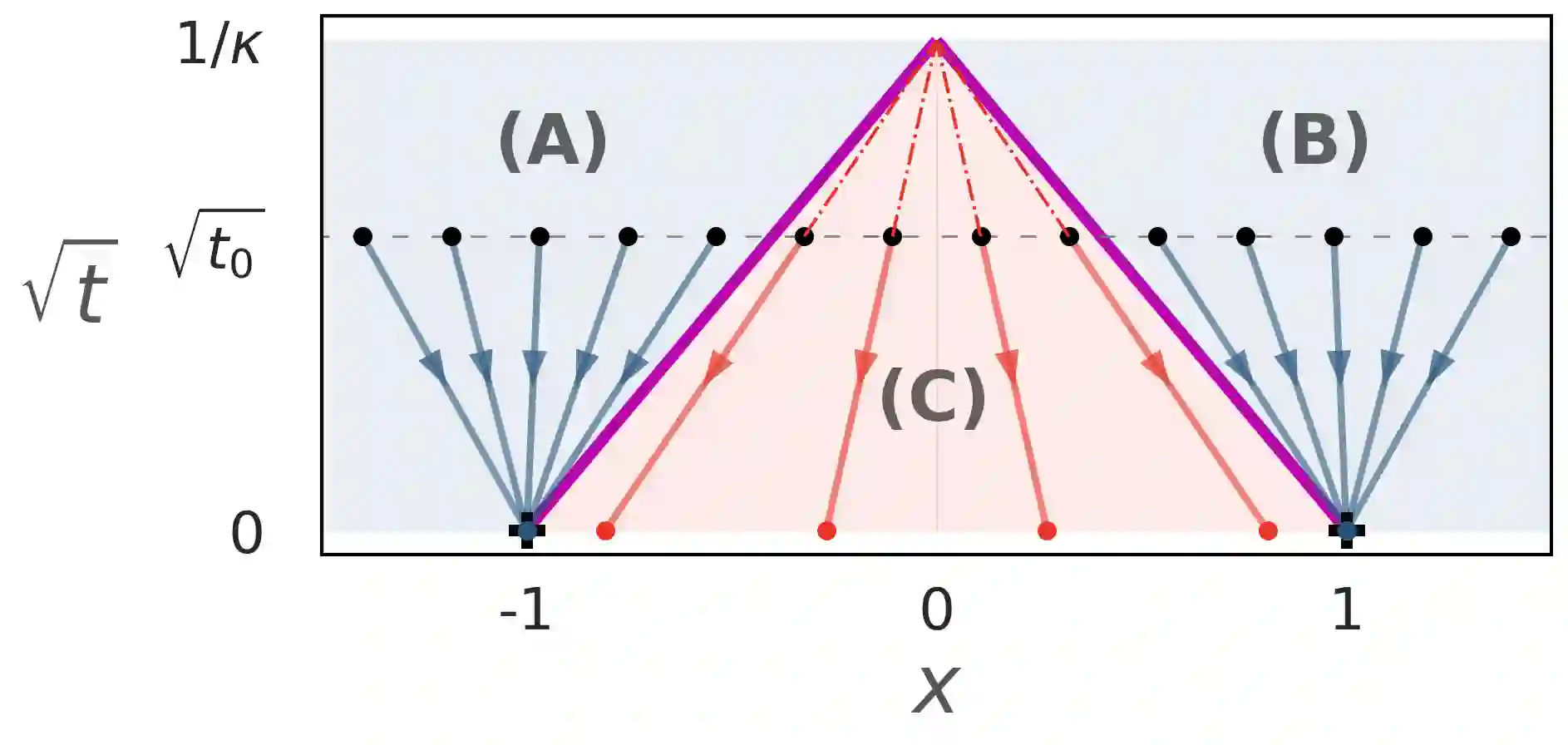
Score-based diffusion models have achieved remarkable progress in various domains with the ability to generate new data samples that do not exist in the training set. In this work, we study the hypothesis that such creativity arises from an interpolation effect caused by a smoothing of the empirical score function. Focusing on settings where the training set lies uniformly in a one-dimensional subspace, we show theoretically how regularized two-layer ReLU neural networks tend to learn approximately a smoothed version of the empirical score function, and further probe the interplay between score smoothing and the denoising dynamics with analytical solutions and numerical experiments. In particular, we demonstrate how a smoothed score function can lead to the generation of samples that interpolate the training data along their subspace while avoiding full memorization. Moreover, we present experimental evidence that learning score functions with neural networks indeed induces a score smoothing effect, including in simple nonlinear settings and without explicit regularization.

翻译：基于分数的扩散模型在多个领域取得了显著进展，能够生成训练集中不存在的新数据样本。本研究探讨以下假设：这种创造性源于经验分数函数平滑化所引起的插值效应。聚焦于训练集均匀分布于一维子空间的情形，我们从理论上证明正则化双层ReLU神经网络倾向于学习经验分数函数的近似平滑版本，并通过解析解与数值实验进一步探究分数平滑与去噪动力学之间的相互作用。特别地，我们论证了平滑分数函数如何能够引导生成沿子空间方向插值训练数据且避免完全记忆的样本。此外，我们通过实验证据表明：使用神经网络学习分数函数确实会诱发分数平滑效应，该现象在简单非线性场景中依然存在，且无需显式正则化。