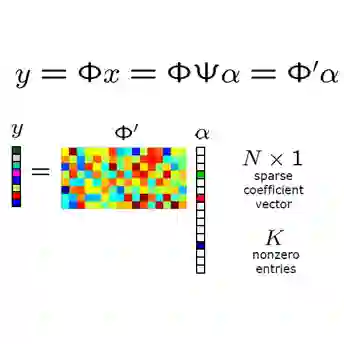
The reconstruction of sparse signals from a limited set of measurements poses a significant challenge as it necessitates a solution to an underdetermined system of linear equations. Compressed sensing (CS) deals with sparse signal reconstruction using techniques such as linear programming (LP) and iterative message passing schemes. The interval passing algorithm (IPA) is an attractive CS approach due to its low complexity when compared to LP. In this paper, we propose a sequential IPA that is inspired by sequential belief propagation decoding of low-density-parity-check (LDPC) codes used for forward error correction in channel coding. In the sequential setting, each check node (CN) in the Tanner graph of an LDPC measurement matrix is scheduled one at a time in every iteration, as opposed to the standard ``flooding'' interval passing approach in which all CNs are scheduled at once per iteration. The sequential scheme offers a significantly lower message passing complexity compared to flooding IPA on average, and for some measurement matrix and signal sparsity, a complexity reduction of 36% is achieved. We show both analytically and numerically that the reconstruction accuracy of the IPA is not compromised by adopting our sequential scheduling approach.

翻译：从有限测量集合中重构稀疏信号是一个重要挑战，因为它需要求解欠定线性方程组。压缩感知（CS）通过线性规划（LP）和迭代消息传递方案等技术处理稀疏信号重构问题。与线性规划相比，区间传递算法（IPA）因其较低复杂度而成为一种颇具吸引力的压缩感知方法。本文提出一种顺序IPA算法，其灵感来源于信道编码中用于前向纠错的低密度奇偶校验（LDPC）码的顺序置信传播译码机制。在该顺序框架中，LDPC测量矩阵Tanner图中的每个校验节点（CN）在每次迭代中按序调度，这与标准“泛洪式”区间传递方法形成对比——后者每次迭代同时调度所有校验节点。相较于泛洪式IPA，顺序方案平均能显著降低消息传递复杂度，针对某些测量矩阵与信号稀疏度，可实现高达36%的复杂度降低。我们通过理论分析与数值实验证明，采用顺序调度策略不会影响IPA算法的重构精度。