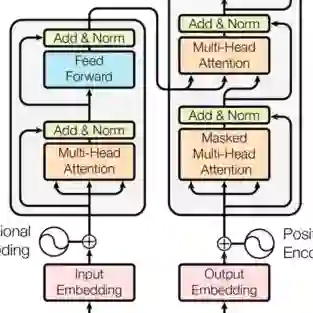
We develop a mathematical framework that interprets Transformer attention as an interacting particle system and studies its continuum (mean-field) limits. By idealizing attention on the sphere, we connect Transformer dynamics to Wasserstein gradient flows, synchronization models (Kuramoto), and mean-shift clustering. Central to our results is a global clustering phenomenon whereby tokens cluster asymptotically after long metastable states where they are arranged into multiple clusters. We further analyze a tractable equiangular reduction to obtain exact clustering rates, show how commonly used normalization schemes alter contraction speeds, and identify a phase transition for long-context attention. The results highlight both the mechanisms that drive representation collapse and the regimes that preserve expressive, multi-cluster structure in deep attention architectures.

翻译：我们建立了一个数学框架，将Transformer注意力机制解释为相互作用的粒子系统，并研究其连续（均值场）极限。通过在球面上理想化注意力机制，我们将Transformer动力学与Wasserstein梯度流、同步模型（Kuramoto）以及均值漂移聚类联系起来。我们结果的核心是一种全局聚类现象：在经历多个聚类排列的长时间亚稳态后，标记会渐近地聚集成簇。我们进一步分析了一个可处理的等角约化模型以获得精确的聚类速率，展示了常用归一化方案如何改变收缩速度，并识别了长上下文注意力的相变。这些结果既揭示了驱动表征崩溃的机制，也指出了在深度注意力架构中保持富有表达力的多聚类结构的参数区域。