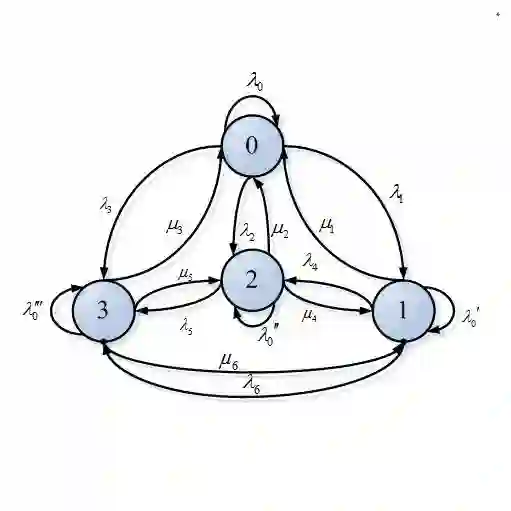
Noninformative priors constructed for estimation purposes are usually not appropriate for model selection and testing. The methodology of integral priors was developed to get prior distributions for Bayesian model selection when comparing two models, modifying initial improper reference priors. We propose a generalization of this methodology to more than two models. Our approach adds an artificial copy of each model under comparison by compactifying the parametric space and creating an ergodic Markov chain across all models that returns the integral priors as marginals of the stationary distribution. Besides the guarantee of their existence and the lack of paradoxes attached to estimation reference priors, an additional advantage of this methodology is that the simulation of this Markov chain is straightforward as it only requires simulations of imaginary training samples for all models and from the corresponding posterior distributions. We present some examples, including situations where other methodologies need specific adjustments or do not produce a satisfactory answer.

翻译：为估计目的构建的无信息先验通常不适用于模型选择与假设检验。积分先验方法是为解决两模型比较时的贝叶斯模型选择问题而发展的，该方法通过修正初始的非正常参考先验来获得先验分布。本文提出将该方法推广至多于两个模型的情形。我们的方法通过紧化参数空间并为每个待比较模型添加人工复制模型，构建一个遍历所有模型的马尔可夫链，该链的平稳分布边缘即为积分先验。除确保其存在性且避免估计参考先验所附带的悖论外，此方法的另一优势在于该马尔可夫链的模拟过程直接明了，仅需对所有模型及其对应后验分布进行虚拟训练样本的模拟。我们展示了若干示例，包括其他方法需要特定调整或无法给出满意解的情形。