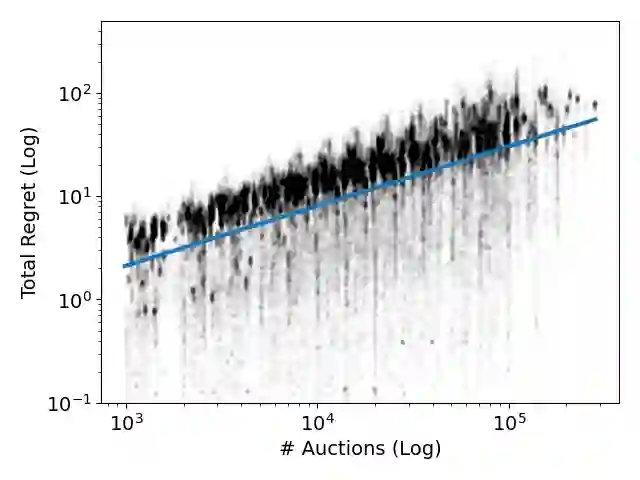
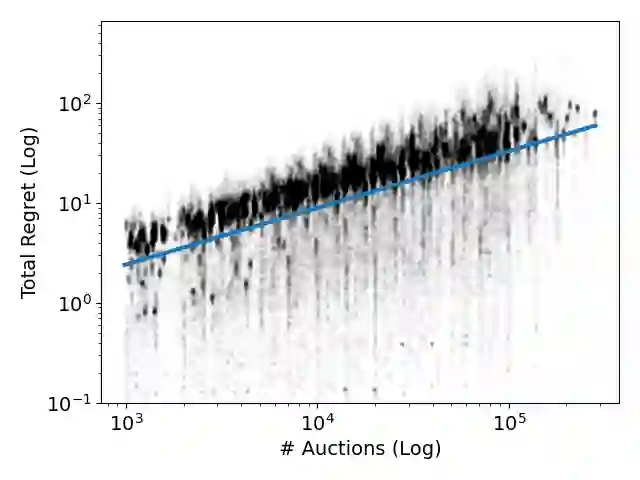
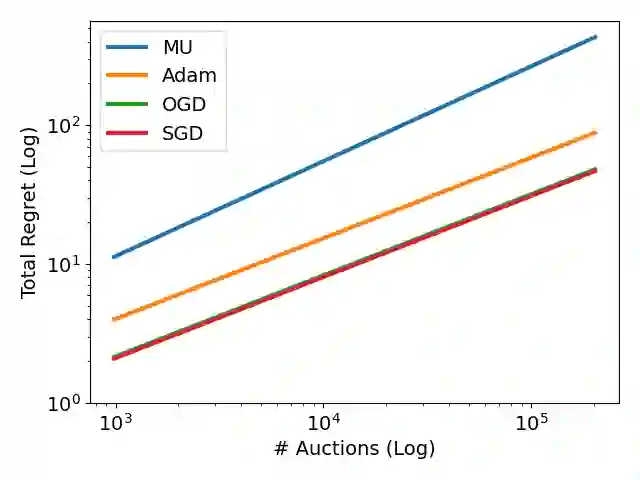
We study the aggregate welfare and individual regret guarantees of dynamic \emph{pacing algorithms} in the context of repeated auctions with budgets. Such algorithms are commonly used as bidding agents in Internet advertising platforms, adaptively learning to shade bids by a tunable linear multiplier in order to match a specified budget. We show that when agents simultaneously apply a natural form of gradient-based pacing, the liquid welfare obtained over the course of the learning dynamics is at least half the optimal expected liquid welfare obtainable by any allocation rule. Crucially, this result holds \emph{without requiring convergence of the dynamics}, allowing us to circumvent known complexity-theoretic obstacles of finding equilibria. This result is also robust to the correlation structure between agent valuations and holds for any \emph{core auction}, a broad class of auctions that includes first-price, second-price, and generalized second-price auctions as special cases. For individual guarantees, we further show such pacing algorithms enjoy \emph{dynamic regret} bounds for individual utility- and value-maximization, with respect to the sequence of budget-pacing bids, for any auction satisfying a monotone bang-for-buck property. To complement our theoretical findings, we provide semi-synthetic numerical simulations based on auction data from the Bing Advertising platform.

翻译：本研究探讨了在预算约束下的重复拍卖场景中，动态调控算法的总体福利与个体遗憾保证。此类算法通常作为互联网广告平台中的竞价代理，通过可调线性乘数自适应地学习调整出价（即"出价抑制"），以实现指定预算的匹配。我们证明，当多个智能体同时采用基于梯度的自然调控策略时，学习动态过程中获得的流动福利至少能达到任何分配规则所能获得的最优预期流动福利的一半。关键在于，该结论在无需动态系统收敛的条件下依然成立，这使得我们能够规避寻找均衡点时已知的计算复杂性障碍。此结果对智能体估值间的相关性结构具有鲁棒性，且适用于任何核心拍卖——这是一类广泛的拍卖形式，包含第一价格、第二价格和广义第二价格拍卖作为特例。在个体保证方面，我们进一步证明此类调控算法在满足单调性价比特性的任何拍卖中，针对预算调控出价序列均能获得个体效用最大化与价值最大化的动态遗憾界。为补充理论发现，我们基于必应广告平台的拍卖数据进行了半合成数值模拟。