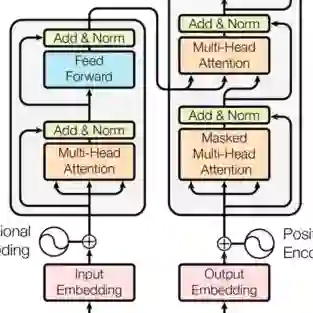
Natural languages exhibit striking regularities in their statistical structure, including notably the emergence of Zipf's and Heaps' laws. Despite this, it remains broadly unclear how these properties relate to the modern tokenisation schemes used in contemporary transformer models. In this note, we analyse the information content (as measured by the Shannon entropy) of various corpora under the assumption of a Zipfian frequency distribution, and derive a closed-form expression for the slot entropy expectation value. We then empirically investigate how byte--pair encoding (BPE) transforms corpus statistics, showing that recursive applications of BPE drive token frequencies toward a Zipfian power law while inducing a characteristic growth pattern in empirical entropy. Utilizing the ability of transformers to learn context dependent token probability distributions, we train language models on corpora tokenised at varying BPE depths, revealing that the model predictive entropies increasingly agree with Zipf-derived predictions as the BPE depth increases. Attention-based diagnostics further indicate that deeper tokenisation reduces local token dependencies, bringing the empirical distribution closer to the weakly dependent (near IID) regime. Together, these results clarify how BPE acts not only as a compression mechanism but also as a statistical transform that reconstructs key informational properties of natural language.

翻译：自然语言在其统计结构上展现出显著的规律性，其中最引人注目的是齐普夫定律与赫普斯定律的出现。尽管如此，这些特性如何与现代Transformer模型中所使用的分词方案相关联，目前仍不甚明确。在本研究中，我们基于齐普夫频率分布的假设，分析了不同语料库的信息量（以香农熵度量），并推导出槽熵期望值的闭式表达式。随后，我们通过实证研究探讨了字节对编码（BPE）如何改变语料库的统计特性，结果表明：BPE的递归应用会推动词频趋向齐普夫幂律分布，同时在经验熵中诱发一种特征性的增长模式。利用Transformer学习上下文相关词符概率分布的能力，我们在经过不同BPE深度分词的语料库上训练语言模型，发现随着BPE深度的增加，模型的预测熵与基于齐普夫定律的预测值趋于一致。基于注意力机制的诊断进一步表明，更深层的分词会减弱局部词符间的依赖性，使经验分布更接近弱依赖（近似独立同分布）状态。综上所述，这些结果阐明了BPE不仅作为一种压缩机制，同时也是一种统计变换手段，能够重构自然语言的关键信息特性。