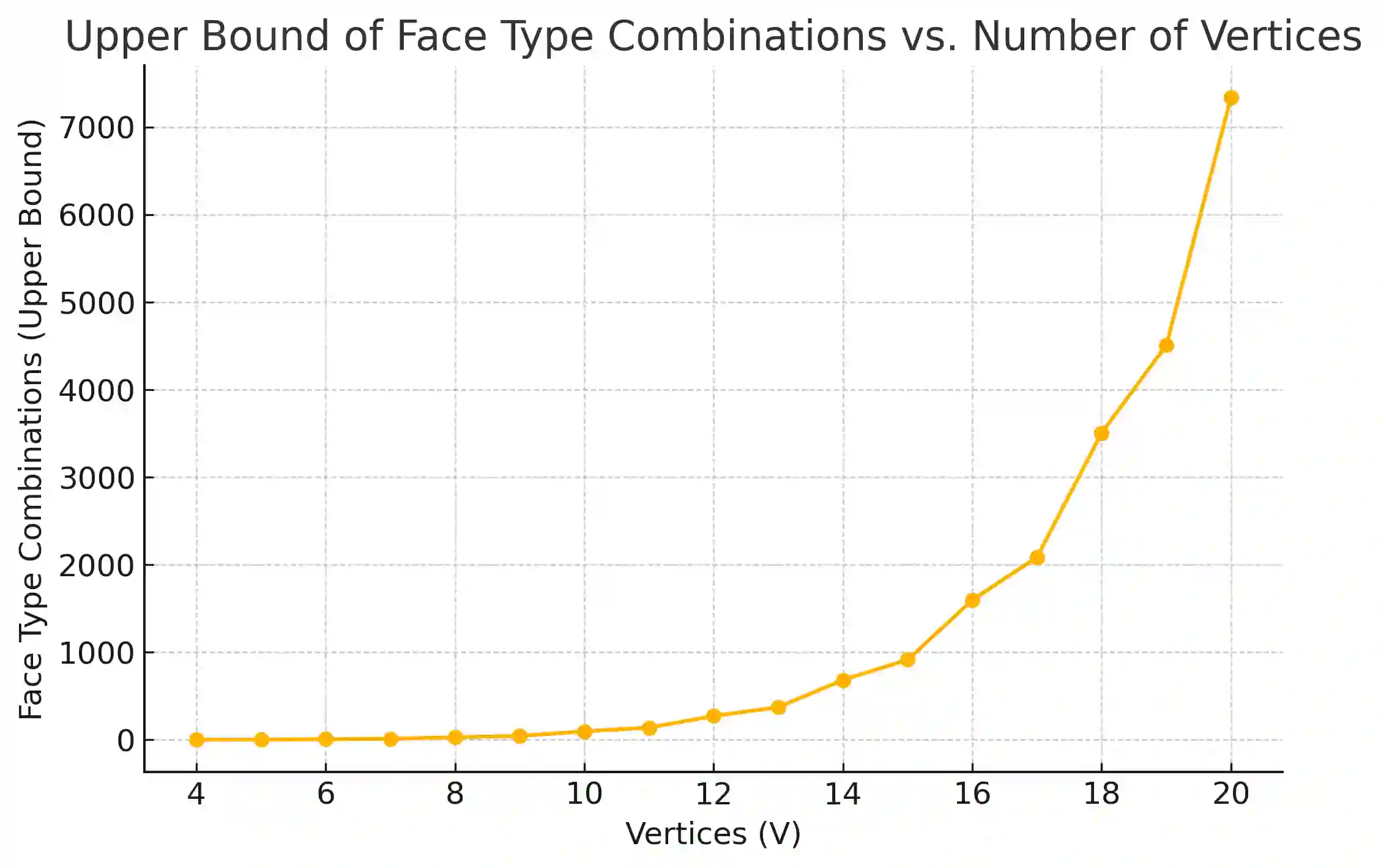
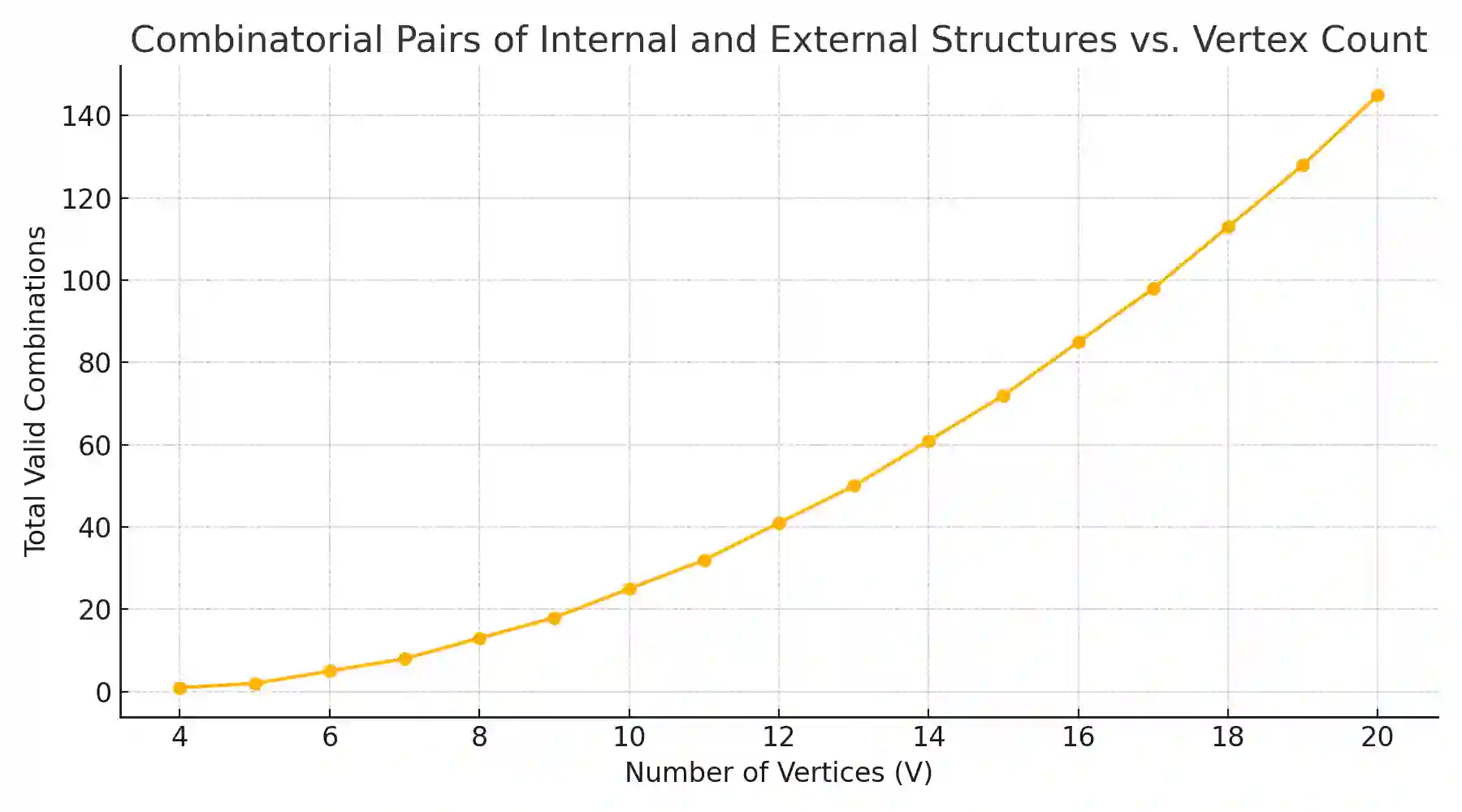
I present a coordinate-free, symbolic framework for determining whether a given set of polygonal faces can form a closed, genus-zero polyhedral surface and for predicting admissible internal tetrahedral decompositions consistent with incidence constraints. The method uses only discrete combinatorial variables, such as the number of tetrahedra T, internal gluing triangles Ni, and internal triangulation segments Si, and applies feasibility checks prior to any geometric embedding. For polyhedra in normal form, I record exact incidence identities linking V, E, and F to a flatness parameter S defined as the sum over faces of (degree minus three), and identify parity-sensitive extremal behavior in E, F, and S arising from minimal vertex-degree constraints. These external identities and parity-dependent bounds hold for genus-zero polyhedral graphs under standard simplicity and connectivity assumptions. For internal quantities, I prove exact relations Ni = 2T - V + 2 and T - Ni + Si = 1, and derive restricted linear ranges for tetrahedral decompositions in normal form with no interior vertices. Together, these results yield a symbolic workflow for rapid pre-screening of combinatorially impossible configurations, reducing reliance on costly geometric validation in computational geometry, graphics, and automated modeling.

翻译：本文提出了一种坐标无关的符号框架，用于判定给定多边形面集能否构成封闭的亏格为零的多面体表面，并预测符合关联约束的容许内部四面体分解。该方法仅使用离散组合变量，如四面体数量T、内部粘合三角形Ni与内部三角剖分段Si，并在任何几何嵌入之前进行可行性检验。对于正规形式的多面体，本文建立了关联顶点数V、边数E和面数F与平坦度参数S（定义为各面度数减三的总和）的精确恒等式，并识别了由最小顶点度约束引起的E、F和S的奇偶敏感极值行为。这些外部恒等式与奇偶依赖的界在标准简单性与连通性假设下对亏格为零的多面体图成立。对于内部参量，本文证明了精确关系式Ni = 2T - V + 2与T - Ni + Si = 1，并推导了无内部顶点时正规形式四面体分解的受限线性范围。综合这些结果，本文构建了一种符号化工作流程，可快速预筛选组合不可行构型，从而减少计算几何、图形学与自动化建模中对昂贵几何验证的依赖。