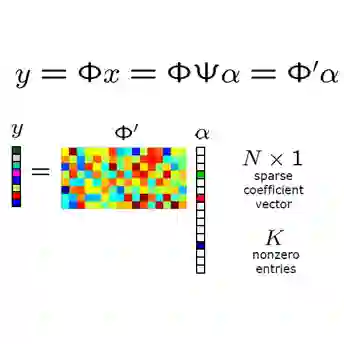
In generative compressed sensing (GCS), we want to recover a signal $\mathbf{x}^* \in \mathbb{R}^n$ from $m$ measurements ($m\ll n$) using a generative prior $\mathbf{x}^*\in G(\mathbb{B}_2^k(r))$, where $G$ is typically an $L$-Lipschitz continuous generative model and $\mathbb{B}_2^k(r)$ represents the radius-$r$ $\ell_2$-ball in $\mathbb{R}^k$. Under nonlinear measurements, most prior results are non-uniform, i.e., they hold with high probability for a fixed $\mathbf{x}^*$ rather than for all $\mathbf{x}^*$ simultaneously. In this paper, we build a unified framework to derive uniform recovery guarantees for nonlinear GCS where the observation model is nonlinear and possibly discontinuous or unknown. Our framework accommodates GCS with 1-bit/uniformly quantized observations and single index models as canonical examples. Specifically, using a single realization of the sensing ensemble and generalized Lasso, {\em all} $\mathbf{x}^*\in G(\mathbb{B}_2^k(r))$ can be recovered up to an $\ell_2$-error at most $\epsilon$ using roughly $\tilde{O}({k}/{\epsilon^2})$ samples, with omitted logarithmic factors typically being dominated by $\log L$. Notably, this almost coincides with existing non-uniform guarantees up to logarithmic factors, hence the uniformity costs very little. As part of our technical contributions, we introduce the Lipschitz approximation to handle discontinuous observation models. We also develop a concentration inequality that produces tighter bounds for product processes whose index sets have low metric entropy. Experimental results are presented to corroborate our theory.

翻译：暂无翻译