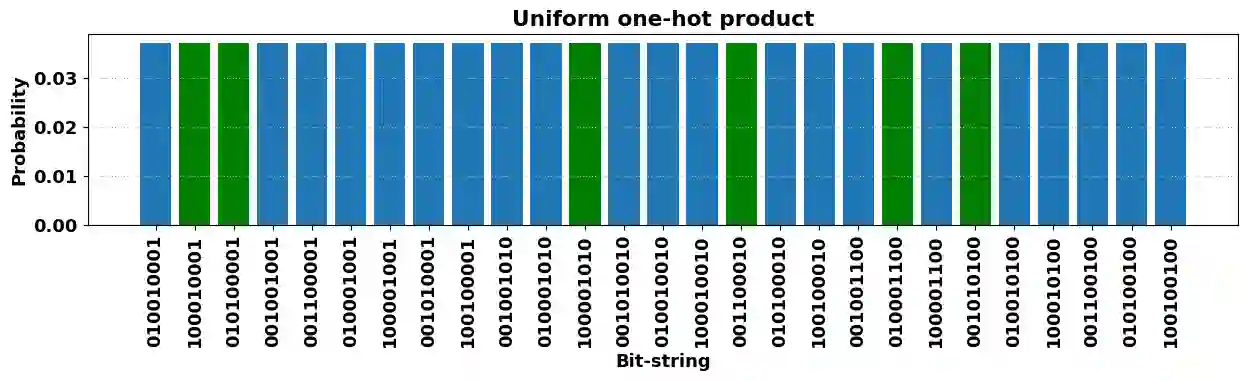
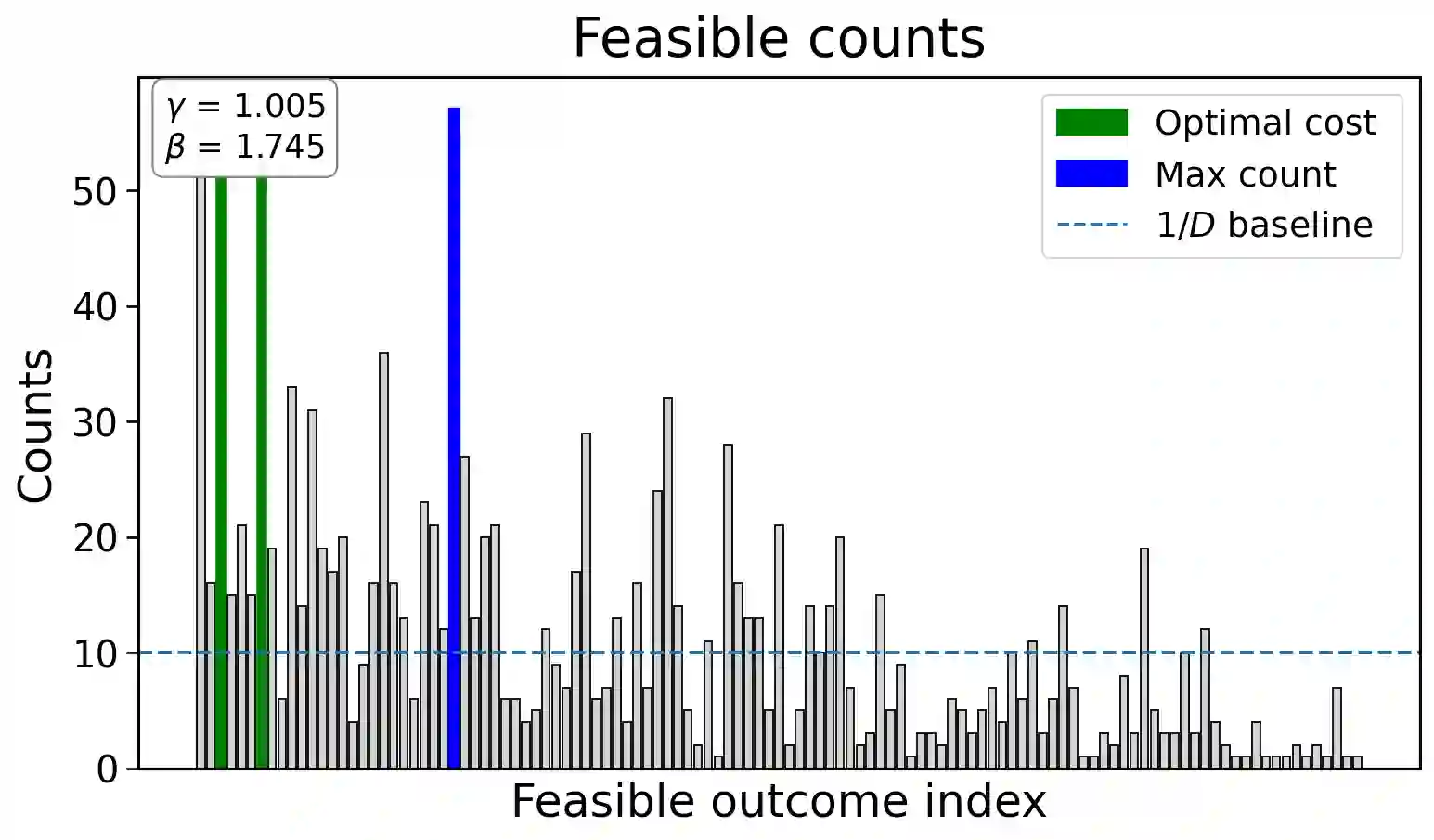
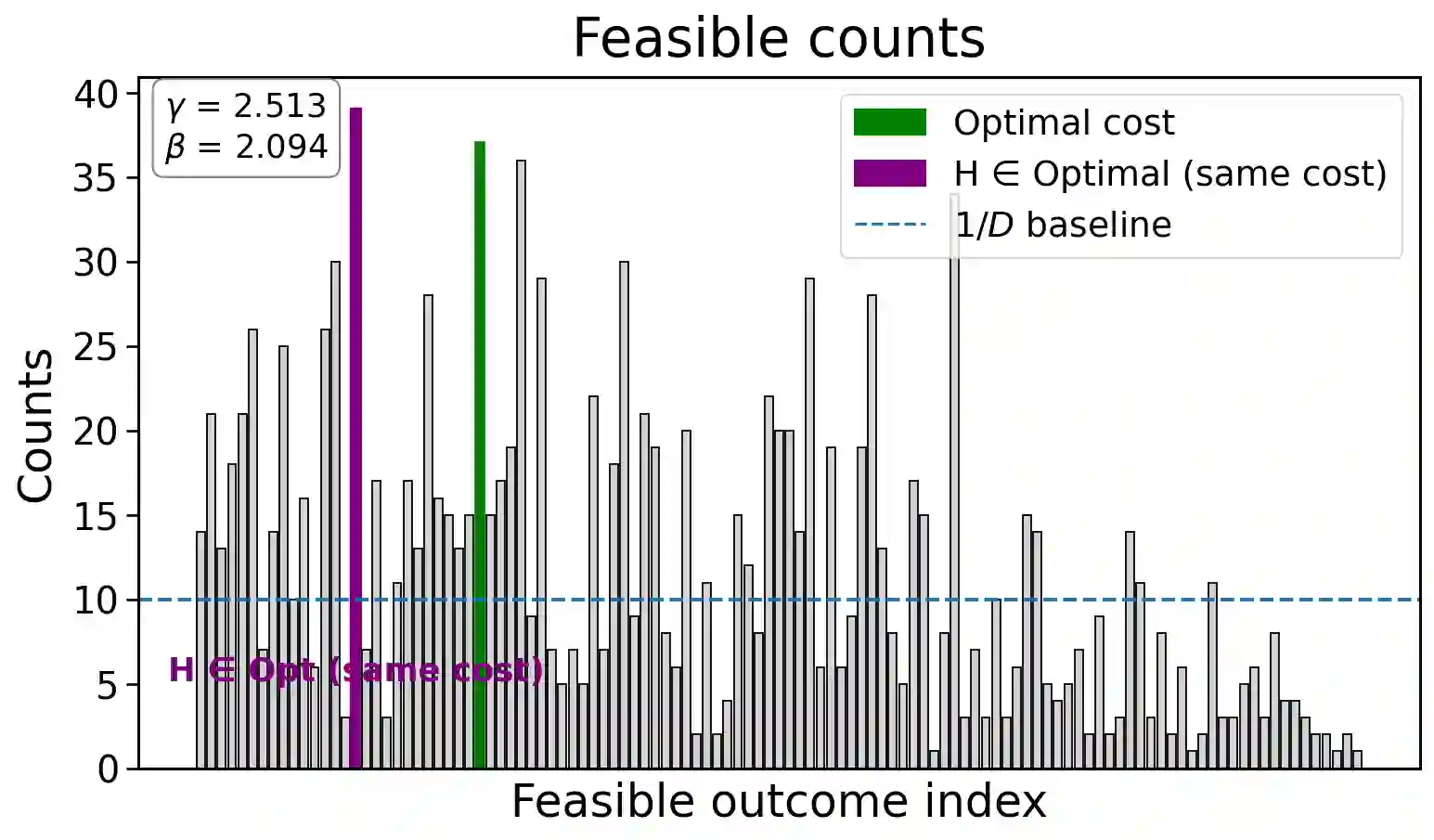
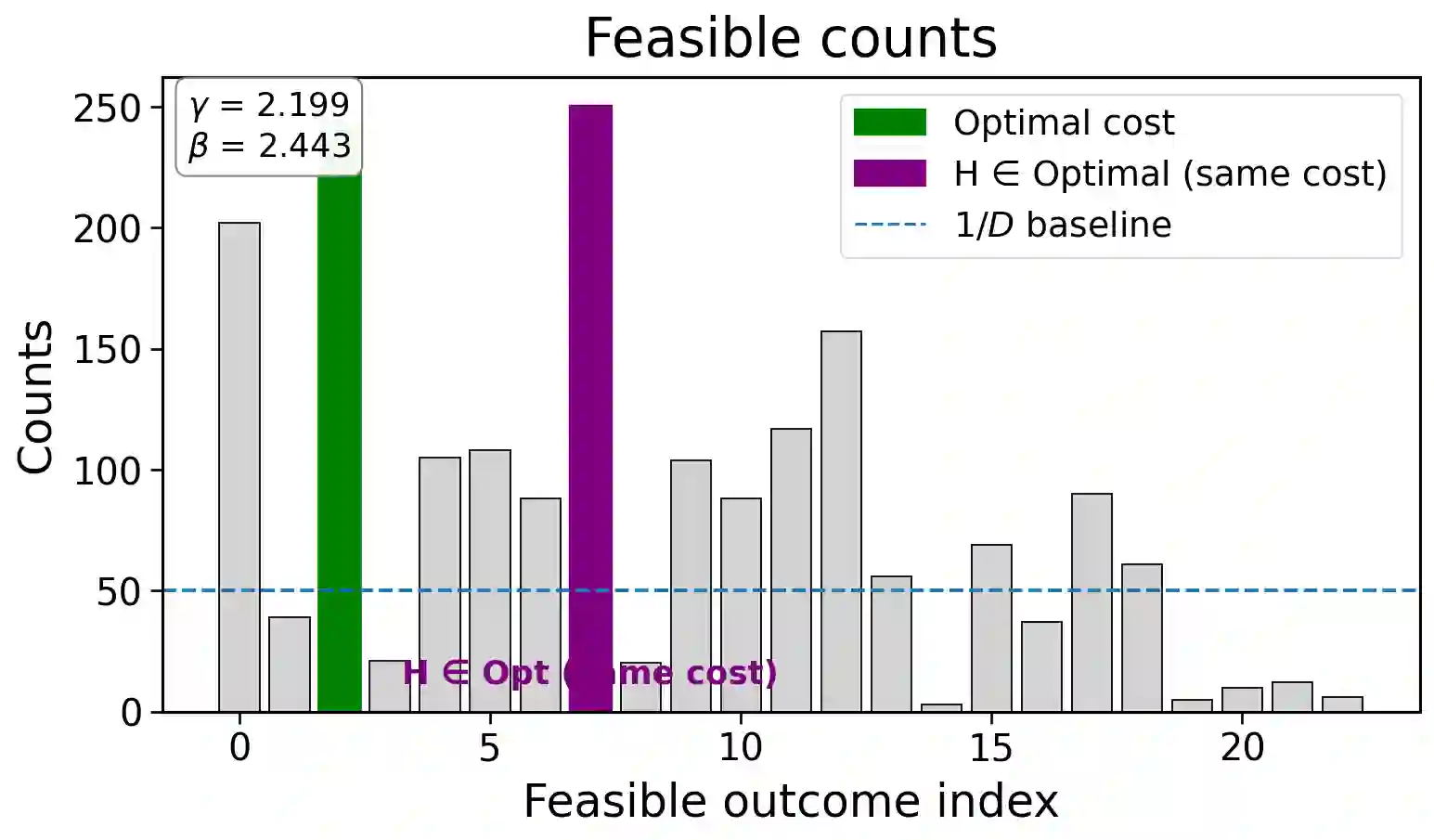
We introduce the Constraint-Enhanced Quantum Approximate Optimization Algorithm (CE-QAOA), a shallow, constraint-aware ansatz that operates inside the one-hot product space [n]^m, where m is the number of blocks and each block is initialized in an n-qubit W_n state. We give an ancilla-free, depth-optimal encoder that prepares W_n using n-1 two-qubit rotations per block, and a two-local block-XY mixer that preserves the one-hot manifold and has a constant spectral gap on the one-excitation sector. At the level of expressivity, we establish per-block controllability, implying approximate universality per block. At the level of distributional behavior, we show that, after natural block and symbol permutation twirls, shallow CE-QAOA realizes an encoded unitary 1-design and supports approximate second-moment (2-design) behavior; combined with a Paley-Zygmund argument, this yields finite-shot anticoncentration guarantees. Algorithmically, we wrap constant-depth sampling with a deterministic feasibility checker to obtain a polynomial-time hybrid quantum-classical solver (PHQC) that returns the best observed feasible solution in O(S n^2) time, where S is a polynomial shot budget. We obtain two advantages. First, when CE-QAOA fixes r >= 1 locations different from the start city, we achieve a Theta(n^r) reduction in shot complexity even against a classical sampler that draws uniformly from the feasible set. Second, against a classical baseline restricted to raw bitstring sampling, we show an exp(Theta(n^2)) minimax separation. In noiseless circuit simulations of traveling salesman problem instances with n in {4,...,10} locations from the QOPTLib benchmark library, we recover the global optimum at depth p = 1 using polynomial shot budgets and coarse parameter grids defined by the problem size.

翻译：本文提出约束增强量子近似优化算法（CE-QAOA），这是一种在单热积空间[n]^m内运行的浅层约束感知拟设，其中m为区块数量，每个区块初始化为n量子比特的W_n态。我们给出一种无需辅助量子比特、深度最优的编码器，该编码器通过每个区块n-1个双量子比特旋转制备W_n态，并采用保持单热流形的双局域块XY混合器，该混合器在单激发子空间具有恒定谱隙。在表达能力层面，我们证明了每区块的可控性，这意味着每区块具有近似通用性。在分布行为层面，我们证明经过自然区块与符号置换扭转操作后，浅层CE-QAOA实现了编码酉1-设计，并支持近似二阶矩（2-设计）行为；结合Paley-Zygmund论证，这为有限采样次数提供了反集中性保证。在算法层面，我们将恒定深度采样与确定性可行性检验器结合，构建了多项式时间混合量子经典求解器（PHQC），该求解器可在O(S n^2)时间内返回观测到的最佳可行解，其中S为多项式级采样次数预算。我们获得了两方面优势：首先，当CE-QAOA固定r≥1个不同于起始城市的位置时，相较于从可行集中均匀采样的经典采样器，我们实现了Θ(n^r)级别的采样复杂度降低；其次，相较于仅限于原始比特串采样的经典基线，我们展示了exp(Θ(n^2))级别的极小极大分离。在基于QOPTLib基准库中n∈{4,...,10}城市规模的旅行商问题实例的无噪声电路模拟中，我们通过多项式采样次数预算和由问题规模定义的粗粒度参数网格，在深度p=1时恢复了全局最优解。